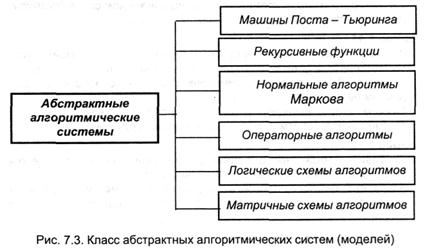
Вернемся к формулировке трудности, решение которой дискуссировалось. Некие теоретические трудности (к примеру, неувязка алгоритмической разрешимости) и потребности практики (к примеру, необходимость формулировки механизмов работы устройств, производящих автоматическую обработку инфы) востребовали построения серьезного определения метода. Разные варианты решения трудности привели к построению так именуемых абстрактных алгоритмических систем (их именуют также алгоритмическими моделями). Рассмотрены только некие из их; их полный список может быть проиллюстрирован схемой изображенной на рис. 7.3. Попробуем узнать, какова связь отдельных моделей.
Все алгоритмические задачки принято разделять на два огромных класса: 1-ый — это задачки, связанные с вычислением значения функции; 2-ой — задачки, связанные с определением принадлежности объекта данному огромному количеству (что равносильно получению ответа на вопрос: обладает ли объект данным свойством?). В первом случае метод Q начинает работать с начальными данными — словом Р, составленным на базе алфавита А, и за конечное число шагов (преобразований) он должен тормознуть и выдать итог Pk = fQ(P). Итог зависит (является функцией) от начального слова, также последовательности обработки, т.е. самого метода. При всем этом вычисление понимается в широком смысле — как алфавитное преобразование.
В задачках, отнесенных ко второму классу, в итоге выполнения метода выходит ответ на вопрос: «Истинно ли выражение, что х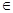 М»? либо, что то же самое, проверяется истинность предиката х
М»? либо, что то же самое, проверяется истинность предиката х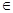 М и выдается один из 2-ух вероятных результатов: Правда либо Ересь. Этот класс можно считать разновидностью первого, так как предикат — это функция, принимающая два значения зависимо от условия. Все же, разделение этих классов задач полезно, потому что приводит к двум принципиальным понятиям теории алгоритмов — вычислимая функция и разрешимое огромное количество.
М и выдается один из 2-ух вероятных результатов: Правда либо Ересь. Этот класс можно считать разновидностью первого, так как предикат — это функция, принимающая два значения зависимо от условия. Все же, разделение этих классов задач полезно, потому что приводит к двум принципиальным понятиям теории алгоритмов — вычислимая функция и разрешимое огромное количество.
Функция именуется вычислимой,если имеется метод, вычисляющий ее значение.
Огромное количество именуется разрешимым,если имеется метод, который для хоть какого объекта позволяет найти, принадлежит он данному огромному количеству либо нет.
Как уже говорилось ранее, данные определения не являются формально серьезными, т.е. не позволяют предсказать, окажется ли некая функция вычислимой либо нет (либо, что тоже самое: как по нраву функции найти, можно ли выстроить метод для ее вычисления?). По этой причине очень принципиальным для построения теории алгоритмов был тезис Черча, который утверждал, что всякая отчасти рекурсивная функция является вычислимой. Другими словами, если функцию удалось простроить при помощи суперпозиции, рекурсии и минимизации из простых арифметических, то существует метод, ее вычисляющий. Дальше последовал тезис Тьюринга, утверждавший, что для всякой вычислимой функции можно выстроить машину Тьюринга, которая ее вычисляет. Можно обосновать, что методы Поста также сводятся к методам, реализуемых при помощи отчасти рекурсивных функций. Справедливо и оборотное утверждение. А именно задачки, решенные для машины Поста в п.7.3.2, являются примером реализации одной из простых рекурсивных функций — функции конкретного следования. Позже была подтверждена аксиома о сводимости одной алгоритмической модели к другой, следствием которой явились утверждения типа: «любую рекурсивную функцию можно вычислить при помощи соответственной машины Тьюринга» либо «для хоть какой задачки, решаемой при помощи машины Тьюринга, существует решающий ее обычный метод Маркова». Таким образом, все модели оказываются эквивалентными, в чем виден глубочайший смысл, ибо итог обработки инфы, непременно, определяется нравом функции (методом) и входными данными, но не находится в зависимости от вида алгоритмической модели.