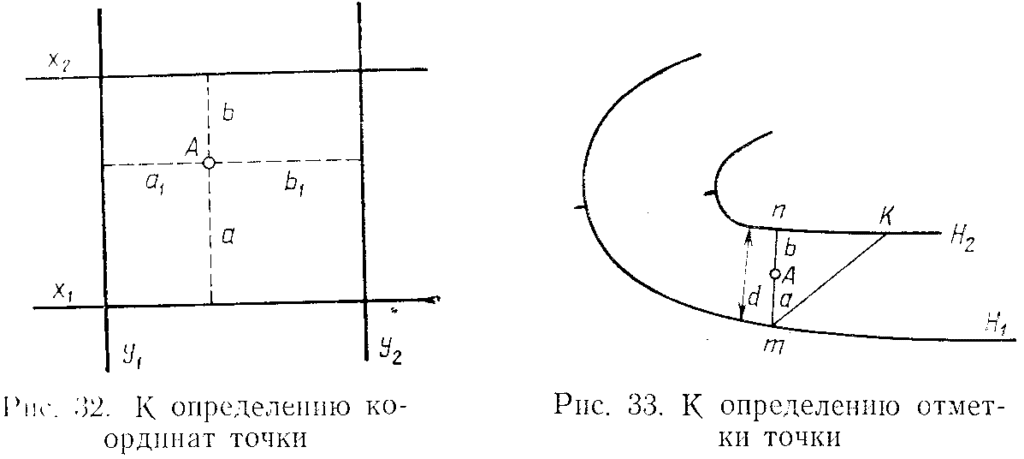
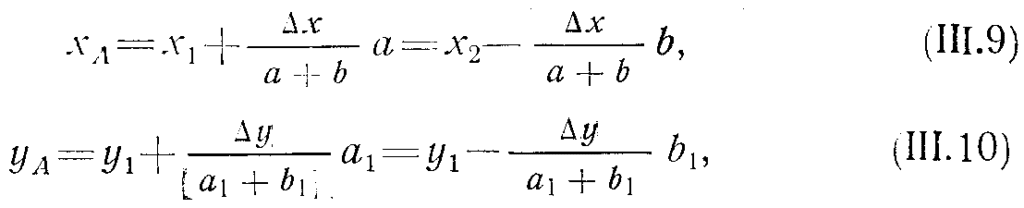Определение координат точки. Пусть точка А (рис. 32) находится в квадрате, абсциссы и ординаты вершин которого x1, x2 и у1, y2.
Проведя через точку А прямые, параллельные осям координат, и измерив с помощью измерителя и масштабной линейки расстояния α, α1 и b,b1 получим:
где Δx = x2 — x1, Δy = y2 — y1.
Определение отметки точки. Если точка лежит на горизонтали, го ее отметка равна отметке этой же горизонтали.
Пусть точка А (рис. 33) лежит между горизонталями с отметками H1 и H2, причем H1 < H2. Проведя через точку А кратчайшую линию между горизонталями и измерив с помощью измерителя и масштабной линейки расстояния d, а и b, получим:
где h— высота сечения рельефа горизонталями.
Определение направления и крутизны ската. Построим линии mn и mk, проведя их между горизонталями с отметками H1 и H2 (рис. 33). Длина линии mn и mk, а вертикальное расстояние между горизонталями (высота сечения рельефа) одно и то же. Следовательно, линия, соответствующая заложению mn, круче линии, соответствующей заложению mk. Отсюда можно сделать вывод, что самому короткому расстоянию между двумя соседними горизонталями соответствует самая крутая линия на местности. Направление этой линии принимается за направления ската, а уклона этой линии служит мерой его крутизны.
Определение уклона линии. Пусть имеются две точки А и В (см. рис. 28), горизонтальное расстояние между которыми равно d, а отметки их равны НА и НB. Тогда согласно формуле (III.1) уклон линии АВ будет:
а уклон линии ВА
Абсолютные значения знаку iAB и iBA равны, но противоположны по знаку.
Определение горизонтальных расстояний. Пусть даны на карте (плане) точки А и В, расстояние между которыми неизвестно. Зная масштаб карты (плана), расстояние АВ можно определить с помощью измерителя и масштабной линейки. Более точно расстояние АВ определяют путем решения обратной задачи на координаты. Для этого вначале по формулам (III.9), (III.10) и (II.13) определяют координаты точек A и B и дирекционный угол направления АВ, а затем по формуле (II.14) вычисляют горизонтальное расстояние АВ.
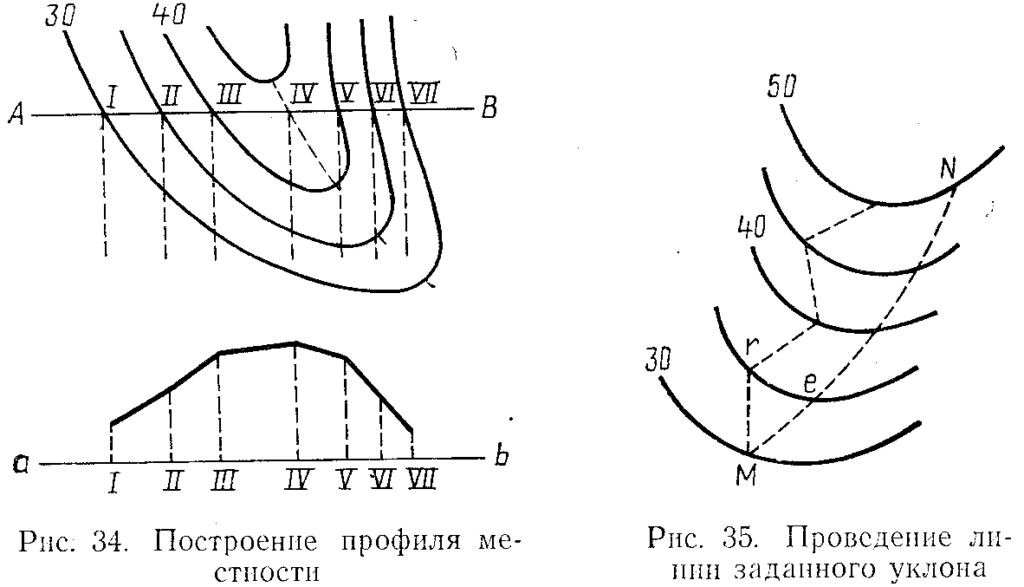
Построение по горизонталям профиля местности. Пусть требуется построить профиль по направлению АВ (рис. 34). Для этого на листе бумаги проводят прямую ab и на ней откладывают расстояния I—II, II—III, …, равные соответствующим расстояниям между горизонталями, определяемыми по направлению АВ. В полученных точках прямой ab восстанавливают перпендикуляры, па которых в произвольном масштабе откладывают высоты точек I, II, …, VII. Соединив концы перпендикуляров прямыми, получают профиль местности по направлению АВ. Для построения профиля вертикальный масштаб принимают крупнее горизонтального в десять раз.
Проведение линии заданного уклона. Допустим, требуется через очки М (рис. 35) и N провести кратчайшую линию так, чтобы уклоны ее отдельных участков не превышали заданного i0.
Подставив в формулу (III.2) вместо h высоту сечения рельефа для данной карты (плана), а вместо i уклон i0, получим кратчайшее расстояние d между горизонталями, которое и будет соответствовать уклону i0. Взяв циркулем в масштабе карты (плана) расстояние d, засекают этим радиусом из точки М следующую горизонталь в точках r и e. Из этих точек тем же радиусом засекают следующую горизонталь и т. д. Следовательно, получают два варианта решения задачи. Направление MeN, как более короткое, принимают за искомое.