Установить рассредоточение разрядов двоичного представления числа типа Real, если для его записи отводится 48 бит, а наибольшее значение десятичного порядка 38. Какова точность обработки таких чисел?
- 2 бита расходуется на запись знака числа и порядка;
- согласно формуле (4.9), k2 = 3.322∙k10; так как k10 = 38, разумеется, наибольший показатель порядка двоичного числа k2 = 3.322∙38 = 12610, что просит в двоичном представлении, согласно формуле Хартли, 7 бит;
- под запись мантиссы отводится 48 — 2 — 7 = 39 бит;
- с учетом укрытого разряда точность обработки составит (39 + 1)/3,322 ≈ 12 десятичных разрядов.
Изначальной предпосылкой появления погрешности обработки кодов вещественных чисел является ограниченность разрядной сетки при их представлении и, как следует, наличие погрешности неизбежно. Но ее величина находится в зависимости от количества имеющихся разрядов и, а именно, уменьшить погрешность можно за счет расширения разрядной сетки, т.е. выделения большего количества ячеек памяти для записи числа. К примеру, в языке PASCAL определен вещественный тип Extended, числа которого занимают 10 б, что обеспечивает точность мантиссы до 20 десятичных символов и значение модуля порядка до 4932. Несколько вариантов представления вещественных чисел в языках программирования высочайшего уровня употребляется как одно из средств оптимизации программки. Увеличение точности вычислений просит огромных ресурсов памяти компьютера; сразу с этим растет и время вычислений. Таким образом, при составлении программки для практической задачки решается неувязка нахождения компромисса меж точностью результата и временем обработки.
В процессе выполнения арифметических действий с нормализованными числами раздельно обрабатываются мантиссы и порядки. Так как операции над кодами вещественных чисел в компьютере владеют некой специфичностью по сопоставлению с обыкновенными арифметическими, будем обозначать их последующим образом: Å — сложение (вычитание), Ä — умножение, Ø — деление.
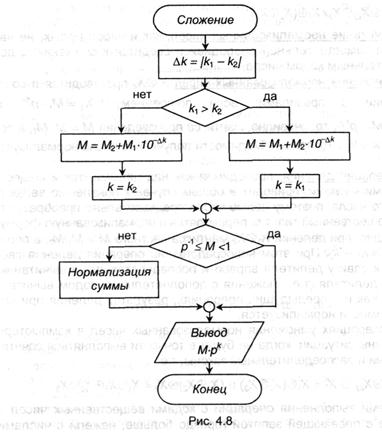
Сложение нормализованных чисел.
Пусть имеются два числа Х1 = М1 ∙ pk1 и Х2 = М2 ∙ рk2 (тут индексы у мантиссы и порядка означают не систему счисления, а служат номерами чисел). Сложение должно начинаться с выявления большего из k1 и k2, нахождения модуля их разности ∆k = |k1 – k2| и сдвига на право на ∆k разрядов мантиссы того числа, у которого k оказался меньше. После чего производится сложение мантисс, порядку результата присваивается значение большего из имеющихся и по мере надобности делается нормализация результата. Метод сложения нормализованных чисел представлен в виде блок-схемы на рис.4.8. При сдвиге на право мантиссы наименьшего числа происходит утрата ∆k младших означающих цифр, что приводит к возникновению погрешности сложения.
Разглядим действие метода на примере сложения десятичных чисел в ограниченной разрядной сетке.