Вернемся к дискуссии того происшествия, что в компьютере для записи числа в хоть какой форме представления отводится конечное число разрядов. Для целых чисел это событие привело к возникновению понятий большего целого числа. Но для каждого целого числа, не превосходящего по модулю большего, имеется ровно одно представление в машинном коде и, если не происходит переполнения, итог выполнения операции над целыми числами будет четким, так как дискретные огромного количества начальных чисел совершенно точно показываются на дискретное огромное количество результатов.
Ситуация конструктивным образом изменяется при представлении и обработке вещественных чисел. На математической числовой оси вещественные числа образуют непрерывное огромное количество (континуум), т.е. два числа могут находиться сколь угодно близко друг к другу, и на любом отрезке содержится нескончаемо много значений чисел. В машинном представлении количество вероятных значений чисел естественно; для двоичной системы счисления оно определяется как 2k, где k — количество двоичных разрядов в представлении мантиссы. Т.е. вещественные числа в компьютере заменяются их кодами, которые образуют конечное дискретное огромное количество; каждый код оказывается представителем целого интервала значений континуума.

Из данного происшествия вытекают ряд следствий:
Следствие 1 заключается в том, что строгие дела меж числами континуума преобразуются в нестрогие для их компьютерных представителей, т.е.
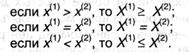
Следствие 2. Так как код вещественного числа в компьютере является ориентировочным представителем многих чисел из интервала, то и результаты вычислений также будут заранее неточными, содержащими неминуемую погрешность. В этом состоит основная особенность обработки вещественных чисел в компьютере — она всегда ведется с погрешностью (кстати, оценка этой погрешности — самостоятельная и сложная задачка).
Следствие 3. Вместе с понятием большего вещественного числа (из-за ограниченности разрядной сетки) возникает понятие меньшего числа либо машинного нуля. К примеру, в типе Real языка PASCAL хоть какое десятичное число, по модулю наименьшее 2,3∙10-39 оказывается машинным нулем, т.е. считается равным 0 при сохранении и в операциях с ним. Таким макаром, математическое понятие «0» как четкое значение числа в компьютерном представлении заменяется понятием «машинный нуль» как значение числа наименьшее некой определенной величины.
Как уже было сказано, основной формой представления кодов вещественных чисел в компьютере является двоичная нормализованная. При всем этом записываться и храниться в памяти компьютера должны все составляющие нормализованной формы (символ числа, мантисса, символ порядка и порядок), что просит нескольких ячеек памяти. К примеру, числа типа Real («вещественный») из языка PASCAL располагаются в 6 б, т.е. 48 двоичных разрядах. Конкретное рассредотачивание компонент нормализованного числа по разрядам определяется конструктивными особенностями компьютера и программным обеспечением. Ниже приведен пример размещения числа в 2-ух ячейках памяти (32 разряда):
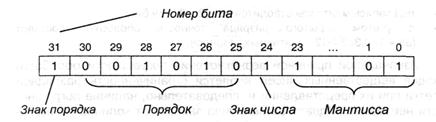
Так как значение мантиссы лежит в интервале 0,12 ≤ М2 < 1, ноль в разряде целых и разделитель десятичных разрядов в представление не врубается, т.е. мантисса содержит только числа дробной части. Более того, можно не сохранять и первую значащую цифру мантиссы, так как она всегда 1 (но, естественно, восстанавливать ее при вычислениях) — это дает возможность хранить дополнительный «скрытый» разряд, т.е. несколько повысить точность обработки. В процессе выполнения арифметических операций, как указывалось ранее, делается нормализация промежных и конечного значений, состоящая в сдвиге мантиссы на право либо налево с одновременным конфигурацией порядка, что эквивалентно смещению разделителя десятичных разрядов — конкретно по этой причине такая форма представления числа получила заглавие «с плавающей запятой». Как и в случае целых чисел, для кодов вещественных чисел существует понятие переполнение, но появляется оно не после наполнения разрядной сетки мантиссы — это приводит только к нормализации числа, а при заполнении всех разрядов порядка. Для представленного выше примера размещения числа в 32-х битах, разумеется,
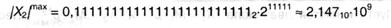
При всем этом точность обработки составит 7 десятичных разрядов. При |Х2| > |X2|max возникнет переполнение, т.е. операция станет неправильной.