Машина Тьюринга состоит из 3-х частей: ленты, считывающая-записывающей головки и логического устройства (рис. 7.1).
Лента выступает в качестве наружной памяти; она считается неограниченной (нескончаемой) — уже это свидетельствует о том, что машина Тьюринга является модельным устройством, так как ни одно реальное устройство не может владеть памятью нескончаемого размера.
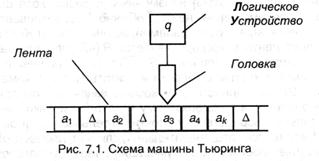
Как и в машине Поста, лента разбита на отдельные ячейки, но, в машине Тьюринга недвижной является головка, а лента передвигается относительно нее на право либо на лево. Другим различием будет то, что она работает не в двоичном, а неком случайном конечном алфавите А = {∆, а1,…ап} — этот алфавит именуется наружным. В нем выделяется особый знак — ∆, именуемый пустым знаком — его посылка в какую-либо ячейку стирает тот символ, который ранее там находился, и оставляет ячейку пустой. В каждую ячейку ленты может быть записан только один знак. Информация, хранящаяся на ленте, изображается конечной последовательностью символов наружного алфавита, хороших от пустого знака.
Головка всегда размещена над одной из ячеек ленты. Работа происходит тактами (шагами). Система исполняемых головкой команд максимально ординарна: на каждом такте она производит подмену знака в обозреваемой ячейке ai знаком aj. При всем этом вероятны сочетания:
- j = i — это значит, что в обозреваемой ячейке символ не поменялся;
- i ≠ 0, j = 0 значит, что хранившийся в ячейке символ заменяется пустым, т.е. стирается;
- i = 0, j ≠ 0 значит, что пустой символ заменяется непустым (с номером j в алфавите), т.е. делается вставка знака;
- i ≠ j ≠ 0 соответствует подмене 1-го знака другим.
Таким образом, в машине Тьюринга реализуется система максимально обычных команд обработки инфы, о которых шла речь в п.7.3.1. Эта система команд обработки дополняется также максимально обычный системой команд перемещений ленты: на ячейку на лево, на ячейку на право и остаться на месте, т.е. адресок обозреваемой ячейки в итоге выполнения команды может или поменяться на 1, или остаться постоянным. Но, хотя практически происходит перемещение ленты, обычно рассматривается сдвиг головки относительно обозреваемой секции — по этой причине команда сдвига ленты на лево обозначается R («Right), сдвига на право — L («Left»), отсутствие сдвига — S («Stop»). В предстоящем будем гласить конкретно о сдвиге головки и считать R, L и S командами ее движения. Элементарность этих команд значит, что по мере надобности воззвания к содержимому некой ячейки, она отыскивается только средством цепочки отдельных сдвигов на одну ячейку. Очевидно, это существенно удлиняет процесс обработки, зато позволяет обойтись без нумерации ячеек и использования команд перехода по адресу, т.е. уменьшает количество поистине простых шагов, что принципиально в теоретическом отношении.
Обработка инфы и выдача команд на запись знака, также сдвига ленты в машине Тьюринга делается логическим устройством (ЛУ). Оно может находиться в одном из состояний, которые образуют конечное огромное количество и обозначаются Q = {q1…qm, z}, при этом, состояние z соответствует окончанию работы, a q1 является исходным (начальным). Q вместе со знаками R, L, S образуют внутренний алфавит машины. ЛУ имеет два входных канала (ai, qi) и три выходных (аi+1, qi+1, Di+1) (см. набросок):

Осознавать схему нужно последующим образом: на такте i на один вход ЛУ подается символ из обозреваемой на этот момент ячейки (ai), а на другой вход — символ, обозначающий состояние ЛУ в данный момент (qi). Зависимо от приобретенного сочетания символов (ai, qi) и имеющихся правил обработки ЛУ производит и по первому выходному каналу направляет в обозреваемую ячейку новый символ (ai+1), подает команду перемещения головки (Di+1 из R, L и S), также дает команду на вызов последующего управляющего знака (qi+1). Таким образом, простой шаг (такт) работы машины Тьюринга заключается в последующем: головка считывает знак из обозреваемой ячейки и, зависимо от собственного состояния и прочитанного знака, делает команду, в какой обозначено, какой знак записать (либо стереть) и какое движение совершить. При всем этом и головка перебегает в новое состояние. Схема функционирования таковой машины представлена на рис. 7.2.
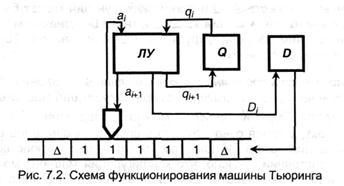
В данной схеме отражено разделение памяти на внешнюю и внутреннюю. Наружняя представлена, как указывалось, в виде нескончаемой ленты — она создана для хранения инфы, закодированной в знаках наружного алфавита. Внутренняя память представлена 2-мя ячейками для хранения последующей команды в течение текущего такта: в Q передается из ЛУ и сохраняется последующее состояние (qi+1), а в D — команда сдвига (Di+1). Из Q по полосы оборотной связи qi+1 поступает в ЛУ, а из D команда поступает на исполнительный механизм, осуществляющий по мере надобности перемещение ленты на одну позицию на право либо на лево.
Общепринятое правило, по которому работает машина Тьюринга, можно представить последующей записью: qiaj→qi‘aj‘Dk, т.е. после обзора знака aj головкой в состоянии ai, в ячейку записывается знак aj‘, головка перебегает в состояние qi‘, а лента совершает движение Dk. Для каждой композиции qiaj имеется роено одно правило преобразования (правил нет только для z, так как, попав в это состояние, машина останавливается). Это значит, что логический блок реализует функцию, сопоставляющую каждой паре входных сигналов qiaj одну и только одну тройку выходных qi‘aj‘Dk — она именуется логической функцией машины и обычно представляется в виде таблицы (многофункциональной схемой машины), столбцы которой обозначаются знаками состояний, а строчки — знаками наружного алфавита. Если символов наружного алфавита п, а число состояний ЛУ т, то, разумеется, общее число правил преобразования составит п∙т.
Определенная машина Тьюринга задается перечислением частей множеств А и Q, также, логической функцией, которую реализует ЛУ, т.е. набором правил преобразования. Ясно, что разных множеств A, Q и логических функций может быть нескончаемо много, т.е. и машин Тьюринга также нескончаемо много.
До этого, чем дискуссировать функционирование машины Тьюринга, введем очередное понятие.
Совокупа состояний всех ячеек ленты, состояния ЛУ и положение головки именуется конфигурацией машины.
Записать конфигурацию можно последующим образом: ∆а1qiaj…аk∆ которая значит, что в слове из k знаков обозревается секция номер j и при всем этом управляющее устройство находится в состоянии qi. Ясно, что конфигурация машины может содержать хоть какое количество знаков наружного алфавита и только один знак внутреннего. Нередко конфигурацию записывают в виде α1qiα2, где α1 — слово на ленте слева от головки, α2 — слово на ленте справа от головки, включая обозреваемый символ. Слева от α1 и справа от α2 лента пуста. Конфигурация, изображенная на рис. 7.1., может быть записана последующим образом: а1∆а2∆qa3а4аk, на рис. 7.2.- 1q1111.
До работы на пустую ленту записывается начальное слово α конечной длины в алфавите А; головка устанавливается над первым эмблемой слова α, ЛУ переводится в состояние q1 (т.е. исходная конфигурация имеет вид q1α). Так как в каждой конфигурации реализуется только одно правило преобразования, исходная конфигурация совершенно точно определяет всю следующую работу машины, т.е. всю последовательность конфигураций прямо до прекращения работы.
Зависимо от исходной конфигурации вероятны два варианта развития событий:
- после конечного числа тактов машина останавливается по команде остановки; при всем этом на ленте оказывается конечная конфигурация, соответственная выходной инфы;
- остановки не происходит.
В первом случае молвят, что данная машина применима к исходной инфы, во 2-м — нет. Вся совокупа входных конфигураций, при которых машина обеспечивает получение результата, образуют класс решаемых задач. Разумеется, использовать машину Тьюринга для задачки, не входящей в класс решаемых, глупо. С другой стороны, в почти всех случаях может быть расширение класса решаемых задач за счет сотворения другой машины Тьюринга. Появляется вопрос: можно ли выстроить такую универсальную машину (хотя бы теоретически), которая решала бы всякую задачку? Тут подошли к вопросу об алгоритмической разрешимости, который будет изучен позже.