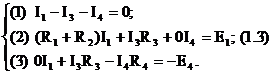Первый закон (правило) Кирхгофа можно сформулировать двояко:
1) алгебраическая сумма токов, сходящихся в любом из узлов схемы, равна нулю:
∑Ik = 0
2) сумма подтекающих к узлу токов равна сумме вытекающих из узла токов:
∑Ik = ∑In
Второй закон Кирхгофа также можно сформулировать двояко:
1) алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС, действующих в том же контуре:
∑IR = ∑E
2) алгебраическая сумма напряжений вдоль любого замкнутого контура равна нулю:
∑Uk = 0
Для решения задачи анализа необходимо составить столько уравнений первого закона Кирхгофа, сколько цепь содержит узлов без одного (y-1), и столько уравнений второго закона Кирхгофа, сколько цепь содержит ветвей без числа уравнений первого закона b — (y-1). Здесь y – число узлов электрической цепи , а b – число ветвей цепи.
При составлении уравнений второго закона Кирхгофа необходимо стремиться выбирать элементарные контуры и помнить о том, чтобы в каждом следующем уравнении появлялась хотя бы одна новая ветвь, не вошедшая ни в одно из предыдущих уравнений. Элементарным называют контур, внутри которого нет ветвей.
Общее количество уравнений Кирхгофа должно соответствовать числу ветвей, которое будет соответствовать числу неизвестных токов.
Расчет токов ветвей по уравнениям Кирхгофа
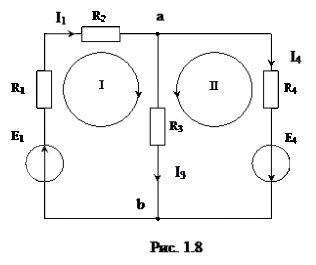
Пусть дана схема (рис. 1.8), в которой заданы: E1,E2,R1,R2,R3,R4. Поставим задачу, определить: I1I3I4.
Составим уравнение (1) по первому закону Кирхгофа для узла (а) и два уравнения (2) и (3) по второму закону Кирхгофа для элементарных контуров I и П. Получим систему уравнений:
Найдем главный определитель системы (1.3):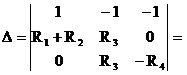
и алгебраическое дополнение: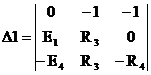 заменяя первый столбец главного определителя столбцом правой части системы (1.3).
заменяя первый столбец главного определителя столбцом правой части системы (1.3).
Решение для тока I1 , будет иметь вид:
I1 = Δ1/Δ
Аналогично замещая столбцом правой части системы (1.3) второй столбец главного определителя, а потом третий получим токи I3 и I4:
I3 = Δ2/Δ, I4 = Δ3/Δ
Таким образом, задача анализа для заданной цепи решена.