Формулировка закона Ома для цепей постоянного тока, которая гласит, что ток в такой цепи прямо пропорционален напряжению на элементе цепи и обратно пропорционален сопротивлению этого элемента постоянному току, протекающему через него.

Однако при изучении цепей переменного тока стало известно, что оказывается кроме элементов цепей с активным сопротивлением, есть элементы цепи с так называемым реактивным сопротивлением, то есть индуктивности и емкости (катушки и конденсаторы).

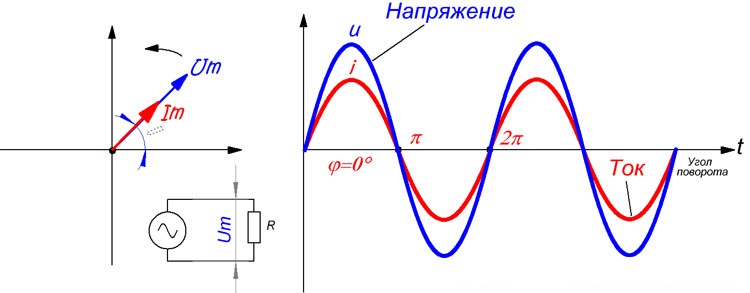
В цепи, содержащей только активное сопротивление, фаза тока всегда совпадает с фазой напряжения (рис 1.), т. е. сдвиг фаз тока и напряжения в цепи с чисто активным сопротивлением равен нулю.

Рисунок 1. Напряжение и ток в цепи с чисто активным сопротивлением. Сдвиг фаз между током и напряжение в цепи переменного тока с чисто активным сопротивлением всегда равен нулю

Отсюда следует, что угол между радиус-векторами тока и напряжения также равен нулю.

Тогда, падение напряжения на активном сопротивлении определяется по формуле:

U_R = I * R (1)

• где, U-напряжение на элементе цепи,
• I – ток через элемент цепи
• R – активное сопротивление элемента

Формула (1) применима как для амплитудных, так и для эффективных значений тока и напряжения:

U_m = I_m * R (2)

• где, Um-амплитудное значение напряжения на элементе цепи,
• Im – амплитудное значение тока через элемент цепи
• R – активное сопротивление элемента

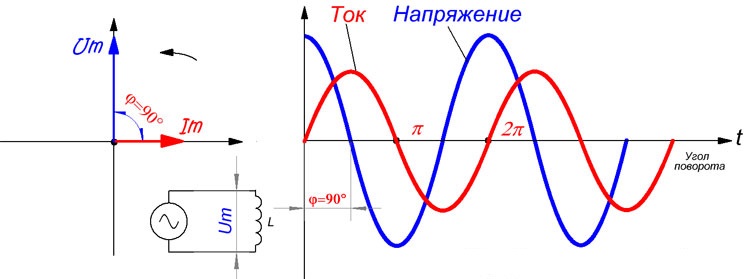
В цепи, содержащей чисто реактивное сопротивление — индуктивное или емкостное, — фазы тока и напряжения сдвинуты друг относительно друга на четверть периода, причем в чисто индуктивной цепи фаза тока отстает от фазы напряжения (рис. 2), а в чисто емкостной цепи фаза тока опережает фазу напряжения (рис. 3).

Рисунок 2. Напряжение и ток в цепи с чисто индуктивным сопротивлением. Фаза тока отстает от фазы напряжения на 90 градусов.

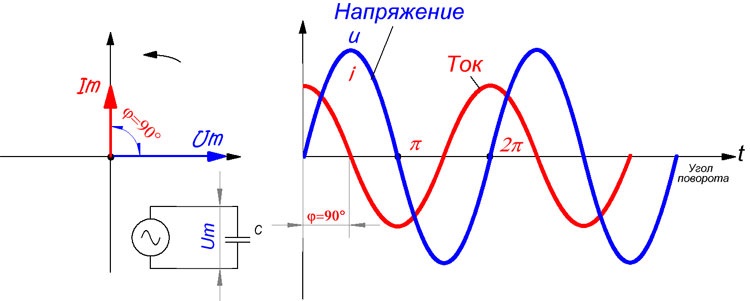
Рисунок 3. Напряжение и ток в цепи с чисто емкостным сопротивлением. Фаза тока опережает фазу напряжения на угол 90 градусов.

Отсюда следует, что в чисто реактивной цепи угол между радиус-векторами тока и напряжения всегда равен 90°, причем в чисто индуктивной цепи радиус-вектор тока при вращении движется позади радиус-вектора напряжения, а в чисто емкостной цепи он движется впереди радиус-вектора напряжения.

Падения напряжения на индуктивном и емкостном сопротивлениях определяются соответственно по формулам:

U_L = I * ωL (3)

U_C = I/ωC (4)

• где U_L — падение напряжение на чисто индуктивном сопротивлении ;
• U_С — падение напряжения на чисто емкостном сопротивлении;
• I — значение тока в через реактивное сопротивление;
• L — индуктивность реактивного элемента;
• C — емкость реактивного элемента;
• ω — циклическая частота.

Эти формулы применимы как для амплитудных, так и для эффективных значений тока и напряжения синусоидальной формы. Однако здесь следует отметить, что они ни в коем случае не применимы для мгновенных значений тока и напряжения, а также и для несинусоидальных токов.

Приведенные выше формулы являются частными случаями закона Ома для переменного тока.

Следовательно, полный закон Ома для переменного тока будет иметь вид:

I = U/Z (5)

Где Z – полное сопротивление цепи переменного тока.

Теперь остается только вычислить полное сопротивление цепи, а оно зависит непосредственно от какие активные и реактивные элементы присутствуют в цепи и как они соединены.

Закон Ома для различных типовых цепей переменного тока

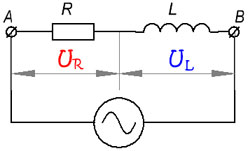
Давайте выясним, как будет выглядеть закон Ома для цепи переменного тока, состоящей из активного и индуктивного сопротивлений, соединенных последовательно (рис. 4.)

Рисунок 4. Цепь переменного тока с последовательным соединением активного и индуктивного сопротивления.

Закон Ома для переменного синусоидального тока в случае последовательного соединения активного и индуктивного сопротивлений выражается следующей формулой:

I = U/Z = U/√(R² + (ωL)²) (6)

• U — эффективное значение напряжения в В;
• R — активное сопротивление в Ом;
• ωL — индуктивное сопротивление в Ом.

Формула (6) будет также действительной, если в нее подставить амплитудные значения тока и напряжения.

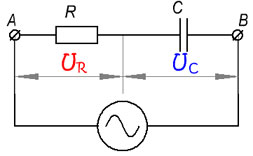
В цепи, изображенной на рис. 5, соединены последовательно активное и емкостное сопротивления.

Рисунок 5. Цепь переменного тока с последовательным соединением активного и емкостного сопротивления.

А закон Ома для такой цепи принимает вид:

I = U/Z = U/√(R² + (1/ωC)²) (7)

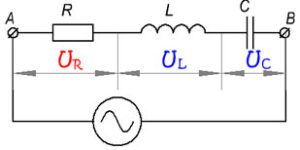
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 6).

Рисунок 6. Цепь переменного тока с последовательным соединением активного, индуктивного и ёмкостного сопротивления.

Закон Ома при последовательном соединении активного, индуктивного и емкостного сопротивлений будет выглядеть так:

I = U/Z = U/√(R² + (ωL — 1/ωC)²) (8)

• где I — сила тока в А;
• U — напряжение в В;
• R — активное сопротивление в Ом;
• ωL — индуктивное сопротивление в Ом;
• 1/ωС — емкостное сопротивление в Ом.

Формула (8) верна только для эффективных и амплитудных значений синусоидального тока и напряжения.

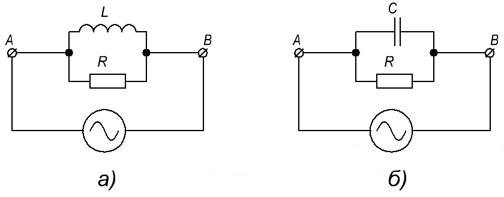
Для того, что бы определить ток в цепях с параллельным соединением элементов (рисунок 7), то необходимо так же вычислить полное сопротивление цепи, как это делать можно посмотреть здесь, затем подставить значение полного сопротивления в общую формулу для закона Ома (5).

Рисунок 7. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) — параллельное соединение R и L; б) — параллельное соединение R и C.

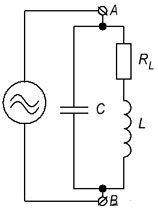
Тоже самое касается и вычисления тока в колебательном контуре изображенном на рисунке 8.

Рисунок 8. Эквивалентная схема колебательного контура.

Таким образом закон Ома для переменного тока можно сформулировать следующим образом.

Значение тока в цепи переменного тока прямо пропорционально напряжению в цепи (или на участке цепи) и обратно пропорционально полному сопротивлению цепи (участка цепи)