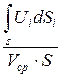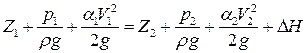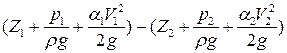Напомним, что уравнение Бернулли для вязкой жидкости отличается от уравнения для идеальной жидкости на значение потерь энергии по пути от одного сечения до другого. Поток жидкости можно представить как сумму элементарных струек, и чтобы записать уравнение Бернулли для потока, необходимо записать его для бесконечного количества элементарных струек и затем просуммировать. Задание это практически невыполнимое, и поэтому, упрощая процесс, проанализируем величины, которые входят в уравнение для элементарной струйки (3.18). Если мы разделим сумму геометрических высот центров тяжести струи на количество струек, получим среднюю величину высоты. Предположим, что она совпадает с координатой центра тяжести живого сечения потока. Будем считать, что Z1 и Z2 – высоты расположения центров тяжести живых сечений потока над плоскостью сравнения. Значение ![]() и
и ![]() принимаем такими же, как и для элементарных струек и откладываем их от координат Z1 и Z2. Со скоростным напором дело обстоит сложней, потому что скорости всех элементарных струек отличаются друг от друга и соответственно кинетические энергии струек также разнятся. Пользуясь условным понятием средней скорости потока, введем поправочный коэффициент, учитывающий неравномерность распределения скоростей по живому сечению потока:
принимаем такими же, как и для элементарных струек и откладываем их от координат Z1 и Z2. Со скоростным напором дело обстоит сложней, потому что скорости всех элементарных струек отличаются друг от друга и соответственно кинетические энергии струек также разнятся. Пользуясь условным понятием средней скорости потока, введем поправочный коэффициент, учитывающий неравномерность распределения скоростей по живому сечению потока:
Этот коэффициент называется коэффициентом Кориолиса и зависит от эпюры распределения скоростей в живом сечении потока. Если эпюра равномерная (прямоугольник), то α = 1. При треугольной и параболической эпюрах α = 2, в эпюрах близких к трапеции α ≈ 1,1. В расчетах турбулентных потоков
α≈1,1; для ламинарных потоков (нефтепроводы, маслопроводы) обычно принимают α ≈ 2. С учетом неравномерности распределения скоростей, уравнение Бернулли для потока реальной жидкости можно записать:
Здесь ∆Н – потери энергии потока на расстоянии между первым и вторым сечениями. Уравнение Бернулли является основным уравнением гидродинамики.
Классификация потерь напора
Потери напора потока между сечениями можно представить в виде:
Потери напора потока – это часть энергии, которая тратится на преодоление сопротивлений при движении потока на пути между двумя сечениями. В общем случае потери напора при движении жидкости складываются из потерь двух видов:
∆Н = Нд + SНм. (3.27)
Здесь Нд – потери напора потока по длине всего трубопровода;
SНм – сумма местных потерь напора.
Потери напора по длине связаны с преодолением сопротивлений, возникающих из-за трения при течении жидкости по прямым участкам трубопроводов.
Местные потери напора обусловлены деформациями формы и направления потока, то есть местные потери возникают только при изменении скорости потока по величине либо по направлению. Для расчета потерь напора по длине трубопровода пользуются зависимостью Дарси-Вейсбаха:
где λ — коэффициент гидравлического (вернее жидкостного) трения (коэффициент Дарси);
ℓ — длина прямого участка трубопровода, м;
d — диаметр трубопровода, м;
V — средняя скорость потока жидкости в трубопроводе, м/с.
Коэффициент гидравлического трения определяется по-разному для различных режимов (зон режимов). Поэтому, чтобы рассчитать потери напора, сначала необходимо определить режим, для чего следует рассчитать значение критерия Рейнольдса.