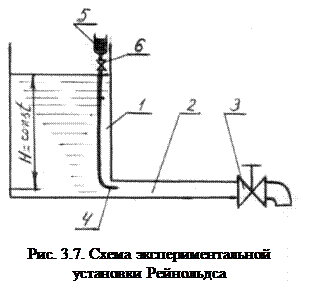
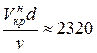Про существование двух принципиально различных режимов движения жидкости инженеры практики догадывались еще в древнее время, но впервые экспериментально подтвердил их существование английский физик Осборн Рейнольдс, опубликовавший в 1883 году результаты исследований наглядно иллюстрировавших наличие этих режимов. Схема простой, но эффективной экспериментальной установки Рейнольдса приведена на рис. 3.7.
Исследовательский стенд состоит из двух резервуаров. Из большого резервуара (1) жидкость попадает в опытную прозрачную трубу постоянного диаметра (2) с регулирующим вентилем (3). Для наглядности в экспериментальную трубу подведена трубочка с краской (4), поступающей из малого бака (5). Расход краски регулируется краном (6). Определение расхода жидкости проходящей через опытную трубу проводится с помощью специального измерительного бачка и секундомера. Экспериментальные исследования начинают с малых скоростей, для чего крану (3) дают самое малое открытие, а краном (6) пускают тонкую струйку краски. В опытной трубе (2) можно наблюдать движение струйки краски в потоке исследуемой жидкости. Струйка краски четко отличается от остального потока, она двигается параллельно стенкам трубы без колебаний и завихрений.
Этот режим движения называется ламинарным (от латинского laminas — слои), частички краски не смешиваются с частицами жидкости соседних струй. Открывая кран (3) немного больше, мы увеличиваем среднюю скорость жидкости в стеклянной трубе, при этом до какого-то граничного значения скорости режим движения струйки краски не изменяется. Однако дальнейшее открытие крана (3), то есть дальнейшее увеличение скорости движения жидкости приводит к тому, что струйка краски начинает колебаться, извиваться и разрываться завихряясь. При дальнейшем увеличении скорости жидкости в трубе заметно возникновение вихрей и, наконец, при еще более увеличенной скорости струйка краски исчезает уже на первых миллиметрах своего пути, но вся жидкость в трубе оказывается равномерно слабо окрашенной. Ламинарный режим перешел в турбулентный (от латинского turbulentus – вихревой, хаотичный) турбулентный режим характеризуется интенсивным перемешиванием частиц жидкости в потоке.
Ламинарный режим переходит в турбулентный всегда при одном и том же определенном значении скорости движения, а если опыты проводить в обратном направлении от турбулентного режима к ламинарному, то этот обратный переход осуществляется при гораздо меньшей скорости. Преодоление инерции хаоса требует большего закрытия крана по сравнению с тем, которое выводит поток из ламинарного режима в турбулентный. Преодолеть инерцию хаоса труднее, чем инерцию порядка. Ламинарный режим наблюдается при течении вязких жидкостей (мед, мазут, нефть, сметана). Течение воды в водопроводных сетях, подача топлива – примеры турбулентного режима.
По результатам опытов Рейнольдс предложил для определения режима течения безразмерный комплекс, который сейчас называют критерием или числом Рейнольдса:
где V – средняя скорость потока, м/с;
d – характерный размер (для трубы — диаметр), м;
ν – кинематическая вязкость жидкости, м2/с.
Критерий Рейнольдса является обязательным условием динамического подобия движения потоков жидкостей и служит для характеристики режима движения потока независимо от вида жидкости. В результате исследований Рейнольдс обнаружил, что при движении в круглых трубах переход от турбулентного режима к ламинарному происходит при:
Здесь Re крн — нижнее критическое значение числа Рейнольдса;
Vнкр — нижняя критическая средняя скорость движения.
Если значение Re < 2320, значит режим движения – ламинарный.
Различают, две критические скорости – нижнюю и верхнюю и, соответственно, два значения числа Рейнольдса. При верхней критической скорости исчезают последние остатки ламинарного режима, остается развитый турбулентный режим. При нижней критической скорости турбулентный режим полностью переходит в ламинарный. Зона между двумя значениями Vкр является переходной зоной, в которой сосуществуют оба режима. Нижнее значение критерия Re стабильно и равно Re = 2320. Значения верхнего критического числа Re различны в различной литературе (от Re = 4000 до Re = 13800). По мнению В.Н.Скрипника Reкрв = 10000.
Современная теория моделирования гидравлических машин базируется на теории гидродинамического подобия. Для подобия двух потоков жидкости необходимо, чтобы числа Рейнольдса обоих потоков были одинаковы. Физический смысл критерия Рейнольдса состоит в том, что число Рейнольдса является условием динамического подобия потоков жидкости.