Для предстоящего рассмотрения нам пригодится ряд определений. Пусть имеются два огромного количества X и Y.
Если неким элементам огромного количества X поставлены в соответствие совершенно точно определенные элементы огромного количества Y, то молвят, что задана частичная функция из X в Y.
Совокупность тех частей огромного количества X, у каких есть надлежащие элементы в Y, именуется областью определения функции, а совокупность тех частей Y, которые соответствуют элементам X, именуются совокупность значений функции.
Если область определения функции из X в Y совпадает с обилием X, то функция именуется везде определенной.
Начальная мысль построения четкого определения метода, опирающегося на понятие рекурсивной функции, заключается в том, что любые данные (непременно, дискретные) можно закодировать натуральными числами в некой системе счисления, тогда и всякое их преобразование сведется к последовательности вычислительных операций, а итог обработки также будет представлять собой целое число. В данном подходе хоть какой метод, единый для данной числовой функции, вычисляет ее значение, а его простыми шагами оказываются обыденные арифметические и логические операции. Такие функции получили заглавие вычислимых.
Пусть имеется класс функций типа у(х1, х2, …, хп), особенностями которых будет то, что все аргументы функции х1,…, хп целочисленны, и значение функции у также выражается целым числом. Другими словами, рассматриваются функции, аргументы и значения которых дискретны.
Функция у(x1, х2, …, хп) именуется отлично вычислимой, если существует метод, позволяющий вычислить ее значение по известным значениям аргументов.
Так как понятие метода в этом определении берется в интуитивном смысле, то и понятие отлично вычислимой функции оказывается интуитивным. Все же, при переходе от алгоритмов к вычислимым функциям появляется одно очень существенное событие. Совокупность процессов, удовлетворяющих условиям 1 — 5 из п. 7.1 и, как следует, подпадающих под интуитивное понятие метода, очень просторная и не достаточно обозрима. Напротив, совокупность вычислимых функций для самых различных осознаний процессов, удовлетворяющих перечисленным условиям, оказалась одной и той же и притом просто описываемой в обыденных математических определениях. Эта точно описанная совокупность числовых функций, совпадающая с совокупностью всех вычислимых функций при самом широком до сего времени известном осознании метода, носит заглавие совокупы рекурсивных функций.
Неважно какая алгоритмическая модель и, в том числе, рекурсивные функции, должна предугадывать определение простых шагов метода и методов построения из их некий последовательности преобразований, обеспечивающих нужную последовательность обработки данных. В рекурсивной модели такими «элементарными шагами» являются так именуемые простые числовые функции S1, 0n и Imn композицией которых строятся все более сложные и которые определяются последующим образом:
- S1(x) = х + 1 — это одноместная (т.е. имеет один аргумент) функция конкретного следования;
- 0n (х1, х2…..xn) = 0 — это n-местная функция, тождественного равенства нулю;
- Imn (x1,…..xn) = xm (1 ≤ т ≤ n; n = 1, 2, …) — п-местная функция тождественного повторения значения 1-го из собственных аргументов.
Перечисленные простые функции везде определены и интуитивно вычислимы. Над ними определяются операции (в предстоящем они именуются операторами), владеющие тем свойством, что их применение к функциям, вычислимым в интуитивном смысле, порождает новые функции, также заранее вычислимые в интуитивном смысле. Частичные функции, которые можно получить с помощью этих операторов из простых функций именуются отчасти рекурсивными. Догадка Черча заключается в том, что класс построенных таким образом отчасти рекурсивных функций совпадает с классом функций, допускающим алгоритмическое вычисление.
Перебегаем к рассмотрению операторов, обеспечивающих преобразование простых функций.
Суперпозиция частичных функций
Пусть m-местные функции

подставляются в n-местную функцию g(x1,…, xn). В итоге выходит n-местная функция
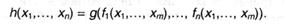
Молвят, что функция h получена из функций g, f1, …, fn суперпозицией (либо подстановкой). Символически такая подстановка обозначается последующим образом: Sn+1(g, f1, …, fn), где индекс сверху обозначает количество функций, подставляемых в качестве аргументов.
Если умеем вычислять функции g, f1, …, fn, то функция h также может быть вычислена. Ясно также, что если все функции g, f1, …, fn везде определены, то и функция h также везде определена. Таким образом, если функции g, f1, …, fn интуитивно вычислимы, то будет интуитивно вычислимой и функция h.