В некой местности имеются две близкорасположенные деревни: А и В. Понятно, что обитатели А всегда молвят правду, а обитатели В — всегда врут. Понятно также, что обитатели обеих деревень обожают ходить друг к другу в гости, потому в каждой из деревень можно повстречать обитателя примыкающей деревни. Путник, сбившись ночкой с пути оказался в одной из 2-ух деревень и, заговорив с первым встречным, возжелал узнать, в какой деревне он находится и откуда его собеседник. Какое малое количество вопросов с бинарными ответами требуется задать путнику?

Количество вероятных композиций, разумеется, равно 4 (путник в А, собеседник из А; путник в А, собеседник из В; и т.д.), т.е. п = 2² и, как следует означает, k = 2. Последовательность вопросов придумайте без помощи других.

Попытаемся осознать смысл приобретенных в данном разделе результатов. Нужно выделить ряд моментов.

1. Выражение (2.14) является статистическим определением понятия «информация», так как в него входят вероятности вероятных исходов опыта. На самом деле дается операционное определение новейшей величины, т.е. устанавливается процедура (метод) измерения величины. Как отмечалось ранее, в науке (научном знании) конкретно таковой способ введения новых определений считается желаемым, так как то, что не может быть измерено, не может быть испытано и, как следует, заслуживает наименьшего доверия.

Выражение (2.13) можно интерпретировать последующим образом: если исходная энтропия опыта Н₁, а в итоге сообщения инфы / энтропия становится равной Н₂ (разумеется, Н₁ ≥ Н₂), то

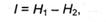
т.е. информация равна убыли энтропии. В личном случае, если вначале равновероятных исходов было п₁, а в итоге передачи инфы / неопределенность уменьшилась, и число исходов стало п₂ (разумеется, п₂ ≤ п₁), то из (2.15) просто получить:

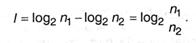
Таким образом, можно дать последующее определение:

Информация — это содержание сообщения, понижающего неопределенность некого опыта с разноплановым финалом; убыль связанной с ним энтропии является количественной мерой инфы.

В случае равновероятных исходов информация равна логарифму дела числа вероятных исходов до и после (получения сообщения).

2. Как уже было сказано, в статистической механике энтропия охарактеризовывает неопределенность, связанную с недочетом инфы о состоянии системы. Большей оказывается энтропия у сбалансированной стопроцентно хаотичной системы — о ее состоянии наша осведомленность мала. Упорядочение системы (наведение какого-то порядка) связано с получением некой дополнительной инфы и уменьшением энтропии. В теории инфы энтропия также отражает неопределенность, но, это неопределенность другого рода — она связана с неведением результата опыта с набором случайных вероятных исходов. Таким макаром, хотя меж энтропией в физике и информатике много общего, нужно сознавать и различие этих понятий. Совсем разумеется, что в предстоящем понятие энтропии будет употребляться в нюансе теории инфы.

3. Следствием аддитивности энтропии независящих опытов (2.5) оказывается аддитивность инфы. Пусть с выбором 1-го из частей (х_A) огромного количества А, содержащего п_A частей, связано /_А = log₂ п_A инфы, а с выбором х_B из В с п_B элементами инфы связано I_B = log₂ п_B и 2-ой выбор никак не связан с первым, то при объединении множеств число вероятных состояний (частей) будет п = п_А ∙ п_B и для выбора композиции х_Aх_B будет нужно количество инфы:

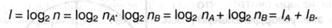
4. Вернемся к утверждению о том, что количество инфы может быть измерено числом вопросов с 2-мя равновероятными ответами. Значит ли это, что I должна быть всегда величиной целой? Из формулы Хартли (2.15), как было показано, I = k бит (т.е. целому числу бит) исключительно в случае п = 2^k. А в других ситуациях? К примеру, при игре «Угадай-ка — 7» (угадать число от 0 до 6) необходимо в выборочном каскаде задать т ≥ log₂ 7 = 2,807, т.е. нужно задать три вопроса, так как количество вопросов — это целое число.

Но представим, что сразу играем в 6 таких же игр. Тогда нужно отгадать одну из вероятных композиций, которых всего

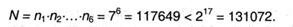
Как следует, для угадывания всей шестизначной композиции требуется I = 17 бит инфы, т.е. необходимо задать 17 вопросов. В среднем на один элемент (одну игру) приходится 17/3 = 2,833 вопроса, что близко к значению log₂ 7. Таким образом, величина I, определяемая описанным выше образом, указывает, сколько в среднем нужно сделать парных выборов для установления результата (полного снятия неопределенности), если опыт повторить неоднократно (n → ).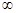

5. Нужно осознавать также, что не всегда с каждым из ответов на вопрос, имеющий только с два варианта ответа (будем дальше именовать такие вопросы бинарными), связан ровно 1 бит инфы. Разглядим опыт, реализующийся средством 2-ух случайных событий; так как их всего два, разумеется, они являются дополнительными друг дружке. Если эти действия равновероятны, р₁ = р₂ = 1/2, и I = 1 бит, как надо из формулы Хартли и (2.14). Но, если их вероятности различны: р₁ = р, то, согласно (А.8), p₂ = 1 — р, и из (2.14) получаем функцию:

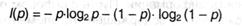
Просто показать, что при р → 0 и при р → 1 функция I(р) → 0. Ситуация может быть проиллюстрирована графиком, из которого, а именно, видно, что кривая симметрична относительно р = 0,5 и добивается максимума при всем этом значении. Если сейчас считать, что событие 1 — это утвердительный ответ на бинарный вопрос, а событие 2 — отрицательный, то приходим к заключению: