Так как одно и то же число может быть записано в разных системах счисления, встает вопрос о переводе представления числа из одной системы (р) в другую (q) — будем обозначать такое преобразование Z_p → Z_q. На теоретическом уровне может быть произвести его при всех q и р. Но схожий прямой перевод будет затруднен тем, что придется делать операции по правилам математики недесятичных систем счисления. По этой причине более комфортными с практической точки зрения оказываются варианты преобразования с промежуточным переводом Z_p → Z_r → Z_q с основанием r, для которого арифметические операции выполнить просто. Такими комфортными основаниями являются r =1 и r = 10, т.е. перевод осуществляется через унарную либо десятичную систему счисления.

Преобразование Z_p → Z₁ → Z_q

Мысль метода перевода максимально ординарна: положим изначальное значение Z_q:= 0; из числа Z_p вычтем 1 по правилам вычитания системы р, т.е. Z_P: = Z_P – 1* и добавим ее к Z_q по правилам сложения системы q, т.е. Z_q:= Z_q + 1; будем повторять эту последовательность действий, пока не достигнем Z_p = 0.

* Символ «:=» употребляется тут и дальше в смысле «присвоить» («считать равным»).

Правила сложения с 1 и вычитания 1 могут быть записаны последующим образом:

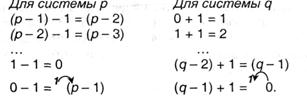
Промежуточный переход к унарной системе счисления в этом случае осуществляется неявно — употребляется упоминавшееся выше свойство независимости значения числа от формы его представления. Рассмотренный метод перевода может быть просто реализован программным методом, а именно, машиной Тьюринга (см. п.7.3.3).