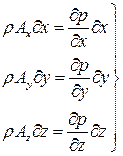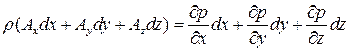Основное уравнение гидростатики. Преобразуем систему уравнений. Для этого умножим первое уравнение на dx, второе – на dy, третье – на dz:

 (2.16)

Сложив левые и правые части уравнения системы, получим дифференциальное уравнение равновесия жидкости:

 (2.17)

Правая часть уравнения представляет собой полный дифференциал давления 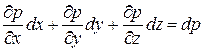, тогда можно записать вместо (2.17):

. (2.18)

Полученное уравнение является основным уравнением гидростатики в дифференциальной форме. Однако, гораздо чаще пользуются уравнением в более простой форме, когда из объёмных сил действует только сила тяжести. В этом случае A_x=0, A_y=0, A_z= — g и уравнение запишется в виде:

dp = -pgdz. (2.19)

Проинтегрировав (2.19), получим основное уравнение гидростатики в виде

p₁ + pgz₁ = const. (2.20)

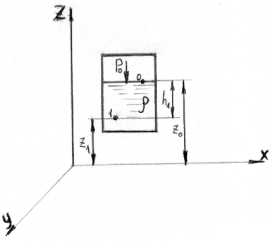
Проиллюстрируем полученное уравнение. Для этого рассмотрим замкнутый сосуд с жидкостью, плотность которой p и на поверхности которой давление р_о^.

Рис. 2.2. Замкнутый сосуд с жидкостью

Выбираем произвольную точку 1, расположенную на высоте z₁. На основании основного уравнения гидростатики (2.20) можно записать:

p₁ + pgz₁ = const. (2.21)

здесь p₁ — гидростатическое давление в точке 1;

z₁ — высота положения выбранной точки над плоскостью сравнения.

Сумма гидростатического давления и произведения ρgz является величиной, постоянной для данного сосуда. Если для сравнения выберем точку 0 на поверхности жидкости, высота которой z₀ , то уравнение (2.21) приобретёт вид:

p₀ + pgz₀ = p₁ + pgz₁,

откуда, (2.22)

где (z₀— z₁)= h₁ глубина погружения точки 1.

Соответственно, давление в произвольной точке будет равно сумме давления на поверхности жидкости плюс давление столба жидкости над этой точкой (2.23):

Полученное уравнение (2.23) – это ещё одна, часто употребляемая формула основного уравнения гидростатики.