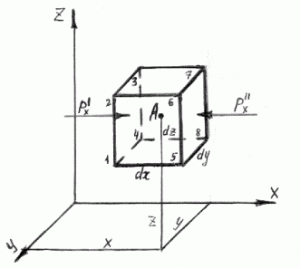
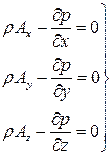Рассмотрим жидкость, находящуюся в равновесии. Выбираем систему произвольных координат с центром в точке O и зафиксируем произвольную точку A с координатами x, y, z (см. рис. 2.1).

Построим вокруг этой точки элементарный параллелепипед с гранями равными: dx, dy, dz. На выделенный объём действуют внешние силы, поэтому он будет находиться в равновесии, если сумма проекций всех действующих сил на каждую ось будет равна нулю. Определим все внешние силы — массовые и гидростатического давления — действующие на грани параллелепипеда со стороны окружающей жидкости. Обозначим проекции массовых сил, отнесенных к единице массы, на координатные оси: Аx, Ay, Az. Тогда проекции массовых сил на ось х.

Рис. 2.1. Элементарный параллелепипед, описанный вокруг точки А.

dFx = Axdm = Axρdxdydz, (2.1)

здесь dm — масса элементарного объёма жидкости

dm = ρdV = ρdxdydz. (2.2)

Аналогично, проекции массовых сил на оси y и z:

dFy = A_ydm = Ayρdxdydz; (2.3)

dFz = Axdm = Azρdxdydz. (2.4)

Теперь рассмотрим силы гидростатического давления, действующие на параллельные грани параллелепипеда 1–2–3–4 и 5–6–7–8. Обозначим силы давления буквами p_x^`и p_x^«. В соответствии с первым свойством гидростатического давления силы давления действуют нормально к поверхностям 1–2–3–4 и 5–6–7–8 и являются силами сжимающими. Если в точке А гидростатическое давление р, то на расстоянии dx/2, на плоскостях 1–2–3–4 и 5–6–7–8 будут действовать давления:

 (2.5)

. (2.6)

где Ϭp/Ϭx– градиент давления на расстояние dx/2 от точки А.

Тогда проекции сил действующие на площади dy*dz поверхностей 1–2–3–4 и 5–6–7–8:

, (2.7)

. (2.8)

Уравнение равновесия параллелепипеда относительно оси Х получим, приравняв к нулю сумму проекций на ось Х всех внешних сил:

. (2.9)

Подставив в уравнение (2.9) значения всех действующих сил получим:

. (2.10)

Раскроем скобки:

. (2.11)

Проведя сокращения и перегруппируя члены уравнения, получим:

. (2.12)

Аналогично получаем уравнения равновесия относительно осей у и z:

. (2.13)

(2.14)

Таким образом, скомпонована система уравнений (2.12, 2.13, 2.14) равновесия жидкости, которую впервые получил Л. Эйлер:

(2.15)