Найти логическую функцию, реализуемую представленной схемой на рис.9.2.
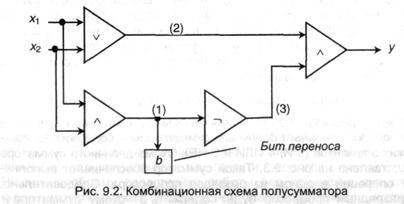
Решение будем вести поочередно, находя значение функции в точках схемы, отмеченных цифрами. Для упрощений используем соотношения из приложения Б.

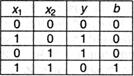
Таким образом, у = x1 Å х2; b = x1 ^ х2). Результаты обработки могут быть представлены в виде таблицы:
Так как перечисленные преобразования являются правилами двоичного суммирования, рассмотренная композиция логических частей получила заглавие полусумматора. На ее вход подаются два сигнала: x1 и х2; выходной сигнал у дает итог сложения в том же двоичном разряде, в каком стоят складываемые числа; в случае суммирования 1 + 1 происходит перенос в старший разряд — для него имеется очередной выход b.
В арифметико-логическом устройстве компьютера полусумматор обрабатывает только младшие разряды регистров. Для всех других разрядов кроме 2-ух складываемых значений нужно учесть бит переноса, образовавшийся в итоге сложения прошлых разрядов. Как следует, комбинационная схема, обеспечивающая выполнение данной операции, обязана иметь три входа (x1, х2 и bi—1) и сформировывать два выходных значения (у и bn) — эта схема именуется двоичным сумматором. Логические функции таковой схемы для каждого из разрядов i (i = 2 … п, считая, что младшим является разряд 1):
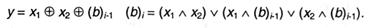
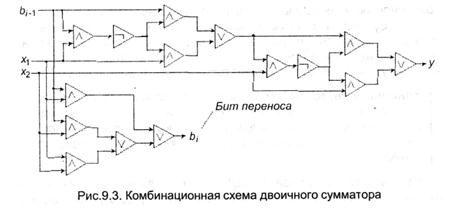
Схема, реализующая такие логические функции — она именуется поочередным двоичным сумматором — содержит 15 логических частей (9 И, 4 Либо и 2 НЕ). Схема двоичного сумматора представлена на рис. 9.3. Таковой сумматор обеспечивает выполнение операций в одном из разрядов микропроцессора. Как следует, 32-разрядный микропроцессор будет содержать 31 схему сумматора и1 полусумматора (для младшего разряда), которые соединены вместе и совместно образуют сумматор.
Схожим образом, вообщем говоря, можно выстроить комбинационную схему для хоть какого конечного огромного количества задач, решение которых (т.е. выходные сигналы) совершенно точно определяются их условием (т.е. входными сигналами). А именно, если ограничиться некой фиксированной точностью представления числа, то можно выстроить комбинационную схему, которая вычисляет значение хоть какой функции у = f(x1,…xn) (непременно, в двоичных кодах), к примеру, sin(x) и др. Но на практике выходит, что при разрядности 32 и выше даже схема умножителя, вычисляющего произведение х1∙х2, становится настолько сложной, что оказывается проще воплотить умножение другим методом, который можно именовать алгоритмическим и который позволяет представить умножение в виде последовательности сложений и сдвигов, о чем шла речь ранее. Точно также и другие вычисления сводятся к цепочкам простых операций: сложение, сдвиг, инверсия и пр.