Какова возможность выкинуть 2 раза по порядку по 6 очков в 2-ух бросках кубика (либо, что эквивалентно, при однократном броске 2-ух кубиков)? Так как р(А) = р(В) = 1/6, то р = 1/6 ∙ 1/6 = 1/36.

Как и в случае сложения вероятностей, формула (А.9) может быть обобщена на случайное число совместных подходящих событий в k независящих опытах. Если вероятности их пришествия в каждом из опытов р₁, p₂,…, p_k, то возможность совместного действия будет равна:

Следствие 3. Так как р_j ≤ 1, разумеется, что р ≤ p_j, т.е. возможность совместного действия не может превосходить возможность хоть какого из их.

Следствие 4. Нахождение среднего для значений случайных независящих величин. Разглядим личную ситуацию, когда случайным событием является числовое значение некой величины. К примеру, число, обозначенное на грани кубика; сумма выигрыша в лотерею; номер этажа, на котором живет человек, масса атома хим элемента и т.п. Пусть этих значений п и они образуют дискретный ряд x₁, х₂, …, x_n. Посреди этих значений возможно окажутся однообразные. Пусть таких групп схожих значений k. Разумеется, k ≤ п. Попробуем отыскать ответ на вопрос: каково среднее значение величины х? К примеру, сколько в среднем очков выпадает при одном броске кубика? Будем исходить из определения среднего значения:

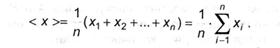
Но эта же сумма может быть получена, если провести суммирование по группам схожих значений:

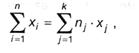
где n_j — количество значений в группе j. Тогда:

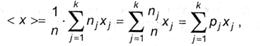
так как отношение п_j/п есть ни что другое, как относительная частота возникновения результата из группы j, которая в пределе (при п→¥) преобразуется в возможность р_j. Таким макаром, совсем получаем, что: