В ящике имеются 2 белоснежных шара и 4 темных. Из ящика извлекают поочередно два шара без возврата. Отыскать энтропию, связанную с первым и вторым извлечениями, также энтропию обоих извлечений. Будем считать опытом α извлечение первого шара. Он имеет два финала: A₁ — вытащат белоснежный шар; его возможность р(А₁) = 2/6 = 1/3; финал А₂ — вытащат темный шар; его возможность р(А₂) = 1 — р(А₁) = 2/3. Эти данные позволяют при помощи (2.4) сходу отыскать Н(α):

Н(α) = — р(А₁)log₂ р(А₁) — р(А₂)log₂ р(А₂) = -1/3 log₂1/3 — 2/3 log₂2/3 = 0,918 бит.

Опыт β — извлечение второго шара также имеет два финала: В₁ — вытащат белоснежный шар; В₂ — вытащат темный шар, но их вероятности будут зависеть от того, каким был финал опыта α. А именно:

при A₁: р_А1(B₁) = 1/5 р_А1(B₂) = 4/5;

при A₂: р_A2(B₁) = 2/5 р_A2(B₂) = 3/5.

Как следует, энтропия, связанная со вторым опытом, является условной и, согласно (2.8) и (2.9), равна:

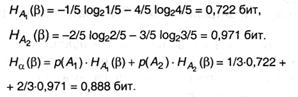
В конце концов, из (2.10): Н(α Ù β) = 0,918 + 0,888 =1,806 бит.