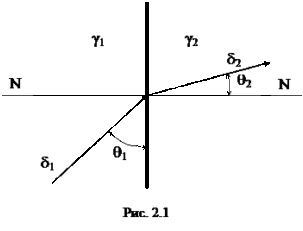
При переходе тока через поверхность раздела сред с различными удельными проводимостями g₁ и g₂ направление тока изменяется, если только линии тока не направлены нормально к поверхности раздела. При этом, на поверхности раздела равны между собой касательные составляющие напряженности поля:

E_t1 = E_t2 (2.4)

и нормальные составляющие вектора плотности электрического тока:

δ_n1 = δ_n2 (2.5)

Здесь индекс 1 относится к первой среде, а индекс 2 – ко второй.

Условия (2.4) и (2.5) можно представить и в таком виде:

E₁sinθ₁ = E₂sinθ₂ и δ₁cosθ₁ = δ₂cosθ₂

Из данных граничных условий можно получить еще одно условие – условие преломления линий поля при переходе их из одного диэлектрика в другой:

tgθ₁/tgθ₂ = γ₁/γ₂, (2.6),

где q₁ и q₂ – углы между вектором напряженности (или плотности тока) и нормалями к границе раздела сред. При этом, если вектор напряженности перпендикулярен к границе раздела, то плотность тока не меняется при переходе из одной среды в другую, а напряженность поля меняется скачком.

Закон преломления линий тока по форме вполне аналогичен закону преломления линий электрического смещения на границе двух диэлектриков в электростатическом поле.

Во многих практических случаях мы встречаемся с переходом тока из металлических тел в окружающую среду, удельная проводимость которой во много раз меньше удельной проводимости материала этих тел. Такие условия имеют место, например, в случае перехода тока через зарытые в землю металлические электроды. Обычно применяют стальные электроды. Удельная проводимость стали приблизительно равна g » 5*10⁶ См/м.

Удельная проводимость почвы зависит от влажности почвы и от ее состава. В среднем ее можно считать равной g » 10^-2 См/м. Таким образом, отношение удельной проводимости материала электродов к удельной проводимости почвы имеет порядок 5*10⁸. Поэтому линии тока со стороны плохо проводящей среды подходят к поверхности электрода примерно под прямым углом.

Во всех таких случаях при рассмотрении поля в среде с малой удельной проводимостью можно пренебречь падением напряжения внутри металлических тел и считать поверхности тел поверхностями равного потенциала.