Случайные действия могут быть описаны с внедрением понятия «вероятность». Соотношения теории вероятностей позволяют отыскать (вычислить) вероятности как одиночных случайных событий, так и сложных опытов, объединяющих несколько независящих либо связанных меж собой событий. Но обрисовать случайные действия можно не только лишь в определениях вероятностей.
То, что событие случаем, значит отсутствие полной убежденности в его пришествии, что, в свою очередь, делает неопределенность в финалах опытов, связанных с данным событием. Непременно, степень неопределенности различна для различных ситуаций. К примеру, если опыт состоит в определении возраста случаем избранного студента 1-го курса дневного отделения университета, то с большой толикой убежденности можно утверждать, что он окажется наименее 30 лет; хотя по положению на дневном отделении могут учиться лица в возрасте до 35 лет, в большинстве случаев очно обучаются выпускники школ ближайших нескольких выпусков. Еще наименьшую определенность имеет аналогичный опыт, если проверяется, будет ли возраст произвольно избранного студента меньше 18 лет. Для практики принципиально иметь возможность произвести численную оценку неопределенности различных опытов. Попробуем ввести такую количественную меру неопределенности.
Начнем с обычный ситуации, когда опыт имеет п равновероятных исходов. Разумеется, что неопределенность каждого из их находится в зависимости от n, т.е. мера неопределенности является функцией числа исходов f(n).
Можно указать некие характеристики этой функции:
- 1. f(1) = 0, так как при п = 1 финал опыта не является случайным и, как следует, неопределенность отсутствует;
- 2. f(n) растет с ростом п, так как чем больше число вероятных исходов, тем паче затруднительным становится пророчество результата опыта.
Для определения очевидного вида функции f(n) разглядим два независящих опыта α и β* с количествами равновероятных исходов, соответственно пα и пβ. Пусть имеет место непростой опыт, который состоит в одновременном выполнении опытов α и β; число вероятных его исходов равно пα ∙ пβ, при этом, они все равновероятны. Разумеется, неопределенность финала такового сложного опыта α ^ β будет больше неопределенности опыта α, так как к ней добавляется неопределенность β; мера неопределенности сложного опыта равна f(nα ∙ nβ). С другой стороны, меры неопределенности отдельных α и β составляют, соответственно, f(nα) и f(nβ). В первом случае (непростой опыт) проявляется общая (суммарная) неопределенность совместных событий, во 2-м — неопределенность каждого из событий в отдельности. Но из независимости α и β следует, что в сложном опыте они никак не могут воздействовать друг на друга и, а именно, α не может оказать воздействия на неопределенность β, и напротив. Как следует, мера суммарной неопределенности должна быть равна сумме мер неопределенности каждого из опытов, т.е. мера неопределенности аддитивна:

* Для обозначения опытов со случайными финалами будем использовать греческие буковки (α, β и т.д.), а для обозначения отдельных исходов опытов (событий) — латинские большие (А, В и т.д.).
Сейчас задумаемся о том, каким может быть очевидный вид функции f(n), чтоб он удовлетворял свойствам (1) и (2) и соотношению (2.1)? Просто узреть, что такому набору параметров удовлетворяет функция log(n), при этом можно обосновать, что она единственная из всех имеющихся классов функций. Таким образом: за меру неопределенности опыта с п равновероятными финалами можно принять число log(n).
Следует увидеть, что выбор основания логарифма в этом случае значения не имеет, так как в силу известной формулы преобразования логарифма от 1-го основания к другому.

переход к другому основанию состоит во внедрении схожего для обеих частей выражения (2.1) неизменного множителя logb а, что равносильно изменению масштаба (т.е. размера единицы) измерения неопределенности. Так как это так, имеется возможность избрать комфортное (из каких-либо дополнительных суждений) основание логарифма. Таким комфортным основанием оказывается 2, так как в этом случае за единицу измерения принимается неопределенность, содержащаяся в опыте, имеющем только два равновероятных финала, которые можно обозначить, к примеру, Правда (True) и Ересь (False) и использовать для анализа таких событий аппарат математической логики.
Единица измерения неопределенности при 2-ух вероятных равновероятных финалах опыта именуется бит*.
* Заглавие бит происходит от британского binary digit,что в дословном переводе значит «двоичный разряд» либо «двоичная единица».
Таким образом, нами установлен очевидный вид функции, описывающей меру неопределенности опыта, имеющего п равновероятных исходов:

Данная величина получила заглавие энтропия. В предстоящем будем обозначать ее Н.
Вновь разглядим опыт с п равновероятными финалами. Так как каждый финал случаен, он заносит собственный вклад в неопределенность всего опыта, но потому что все п исходов равнозначны, уместно допустить, что и их неопределенности схожи. Из характеристики аддитивности неопределенности, также того, что согласно (2.2) общая неопределенность равна log2 п, следует, что неопределенность, вносимая одним финалом составляет
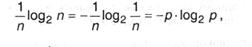
где р = — возможность хоть какого из отдельных исходов.
Таким образом, неопределенность, вносимая каждым из равновероятных исходов, равна:
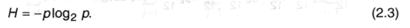
Сейчас попробуем обобщить формулу (2.3) на ситуацию, когда финалы опытов неравновероятны, к примеру, р(А1) и р(А2). Тогда:
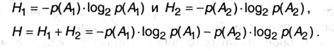
Обобщая это выражение на ситуацию, когда опыт α имеет п неравновероятных исходов А1, А2… Ап, получим:
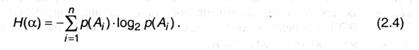
Введенная таким образом величина, как уже было сказано, именуется энтропией опыта ос. Используя формулу для среднего значения дискретных случайных величин (А.11), можно записать:
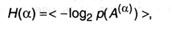
А(α) — обозначает финалы, вероятные в опыте α.
Энтропия является мерой неопределенности опыта, в каком появляются случайные действия, и равна средней неопределенности всех вероятных его исходов.
Для практики формула (2.4) принципиальна тем, что позволяет сопоставить неопределенности разных опытов со случайными финалами.