Размеры двух любых деталей, взятых из одной партии, различны. У деталей одной партии, изготовленных в одинаковых условиях, можно установить максимальное значение разности их размеров, или поле рассеивания размеров. Он охарактеризует точность выбранного метода обработки для данных производственных условий.
Неточность обработки поверхностей является результатом влияния различных факторов, которые вызывают погрешности. Теорией и практиком технологии машиностроения установлено, что действие этих факторов характеризуется полем рассеивания размеров и законом распределения размеров (кривая распределения и характеризующие ее параметры). На основании этого закона при решении практических задач, касающихся точности обрабатываемых заготовок, применяют методы, рекомендуемые математической статистикой и теорией вероятности. Пользуясь этими методами, можно расчетно-аналитическим путем определить наиболее вероятные значения размеров обрабатываемой заготовки при данных условиях обработки.
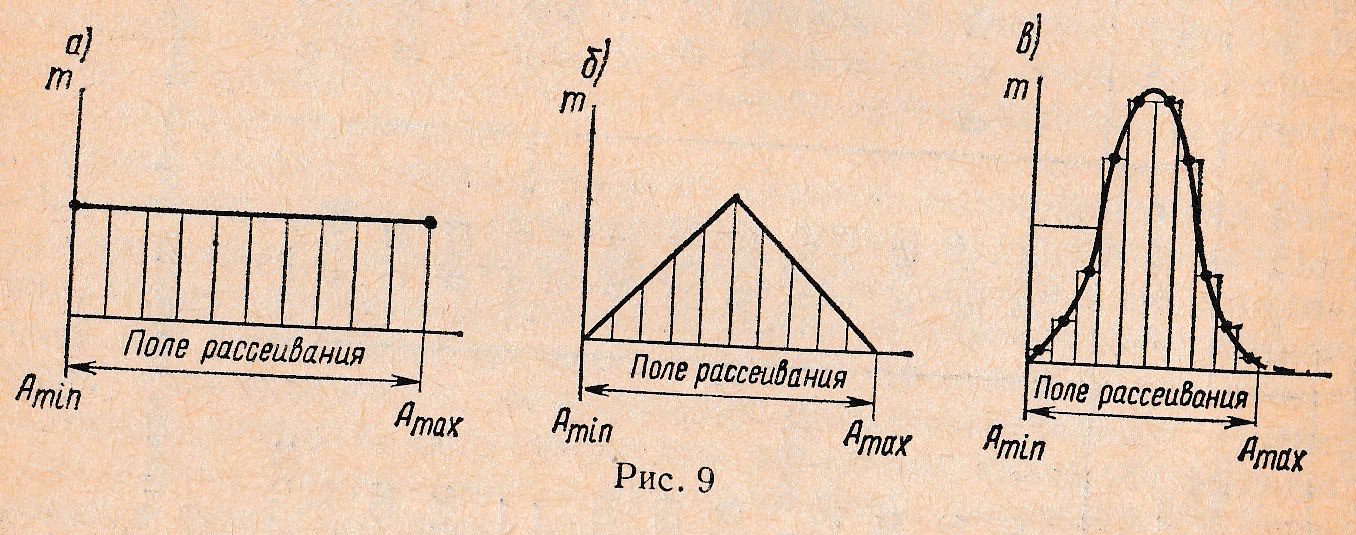
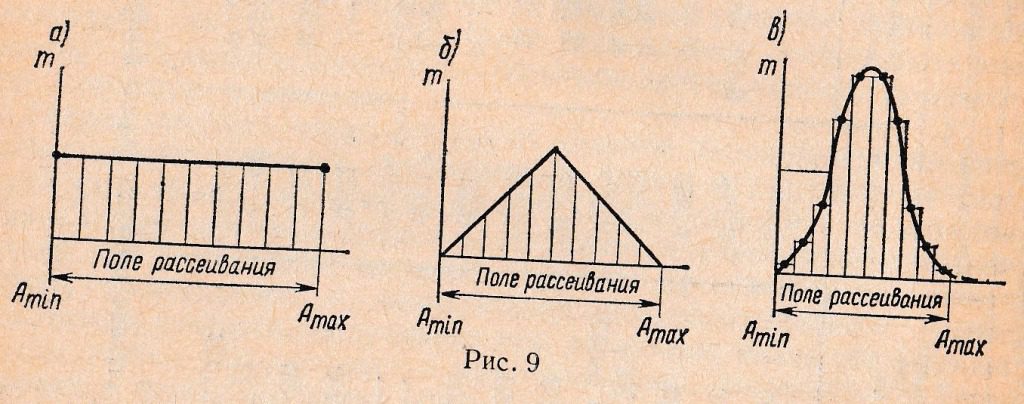
Измеряя размеры деталей одной партии после обработки их на станке, можно в пределах установленного допуска на размер разделить их на несколько групп с размерами в пределах определенного интервала. Тогда при достаточно большой партии деталей (50… 100 шт.) можно обнаружить, что число деталей в группах различно. Если построить график, расположив по горизонтали номера групп с последовательно возрастающими размерами от АMIN до AMAX установленного интервала (рис. 9), а по вертикали — число заготовок m, попавших в каждую группу и характеризующих частоту повторения размеров, то получившаяся кривая выразит закон распределения размеров деталей в данной партии. Если n — число деталей в партии, то отношение m/n называют частостью появления случайного события (в данном случае деталей одной категории точности).
В зависимости от степени влияния различных факторов, действующих в процессе получения размеров, можно получить весьма разнообразные формы кривых, характеризующих законы распределения. Наиболее характерными являются: кривая распределения по закону равной вероятности, кривая распределения по закону Симпсона и кривая распределения по закону Гаусса, или, как часто его называют, закону нормального распределения.
Закон равной вероятности получения размеров деталей одной партии показывает, что при выбранных методе обработки и оборудовании размер зависит только от одного из факторов, например, износа режущего инструмента. Если износ инструмента при этом нарастает во времени по прямолинейному закону, размер обрабатываемой заготовки изменяется также строго постоянно, увеличиваясь или уменьшаясь (рис. 9, а). Однако, это возможно, если действия всех остальных факторов несущественны и не влияют на изменение размеров заготовок. Если жесткость технологической системы недостаточна, и в связи с износом элементов системы появляется дополнительная ее деформация, и) размер детали может изменяться во времени уже по другому закону. При суммарном действии этих двух факторов закон распределения размера деталей имеет форму треугольника — закон Симпсона (рис. 9, б). Если влияние всех факторов в процессе обработки заготовок одинаково и ни один из них не является ярко выраженным, получение наперед заданного размера в данный момент времени при изготовлении данной партии деталей не может быть обеспечено. Однако при этом представляется возможным установить наиболее вероятный ожидаемый размер заготовок в данной партии по закону Гаусса (рис. 9, б). Этот размер располагается в середине поля рассеивания, которое и характеризует технологический процесс, выбранный для обеспечения заданного размера.