Какова возможность вытащить козыря либо туза из колоды 36 карт, если козырной объявлена одна из мастей?
Событие А — получение козыря — имеет возможность р(А) = 9/36 = 1/4, так как карт одной масти 9. Событие B — получение туза — имеет возможность р(В) = 4/36 = 1/9, так как тузов 4; но из их один — козырный (т.е. реализуются и А и B); возможность его возникновения р(А ^ В) = р(A) ∙ р(B) = 1/36. Тогда, согласно (А.13), р(А ^ В) = р(А) + р(В) — р(A) ∙ р(В) = 1/4 + 1/9 — 1/36 = 12/36 = 1/3
Сейчас при нахождении вероятности произведения событий р(A ^ B) попробуем учитывать то событие, что действия А и В не непременно могут быть независящими — разумеется, это более общий случай. Отсутствие независимости случайных событий значит, что одно из их влияет на другое, т.е. возможность второго действия находится в зависимости от того, вышло ли 1-ое. К примеру, вы случаем повстречали знакомого на вечеринке (событие В); но решение пойти на эту вечеринку (событие А) вы приняли случаем, выбирая из нескольких способностей; таким макаром, случайное событие В оказывается следствием случайного действия А.
Возможность действия В при условии, что влияющее на него событие А имело место, именуется условной вероятностью.
Обозначать условную возможность будем рА(В). Объективности ради следует увидеть, что возможность хоть какого случайного действия находится в зависимости от каких-либо критерий, при которых может быть его пришествие либо ненаступление. К примеру, условием того, что возможность выпадения всех цифр игральной кости схожа и равна 1/6, является ее верная геометрическая форма и однородность материала. Если условия поменяются (к примеру, форма будет не куб, а параллелепипед), то поменяется и возможность. Просто договорились считать возможность событий, для которых условия не меняются в разных сериях опытов, бесспорной; если же условия могут изменяться — употребляется термин «условная вероятность». Довольно естественным представляется также утверждение: если А и B независимы, то рA(В) = р(В). Более того, данное утверждение можно считать математически четким определением понятия «независимые события»;
Два случайных действия А и В являются независящими, если их условные вероятности равны бесспорным, т.е. рА(В) = р(В) и рВ(А) = р(А).
Пусть из п равновероятных исходов событие А реализуется т методами, из которых k являются подходящими и для пришествия действия В, связанного с А. Тогда, разумеется:
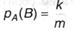
Возможность совместного выполнения событий А ^ В равна
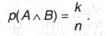
Но
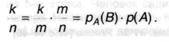
Совсем имеем:
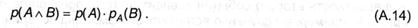
Приобретенное выражения является более общим правилом умножения вероятностей; выражение (А.9), разумеется, оказывается личным случаем (А.14) при условии, что А и B независимы. Подстановка приобретенного выражения в формулу (А.12) позволяет получить общепринятое правило сложения вероятностей:
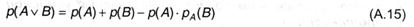
Перечислим (без подтверждения) некие характеристики условной вероятности:
- условная возможность рA(iB) может быть как больше бесспорной р(В), так и меньше ее (т.е. событие А может как понижать возможность В, так и увеличивать ее); но, всегда 0 ≤ РA(B) ≤ 1. Для ситуации, когда А с необходимостью тянет за собой В (к примеру, А — выпадение четверки при бросании игральной кости, а B — выпадение четной числа) будем использовать обозначение «Ì» (А Ì B — читается «A тянет B»). Разумеется, если А Ì B, то рA(B) = 1. Если А и B несовместны, рА(В) = 0;
- если B Ì B‘, то рА(В) ≤ рA(B‘);
- для дополнительных событий рA(В) = 1 – pA(B);
- если B и С несовместны, то pA(B v С) = рА(В) + рА(С).
Имеется три урны, содержащие белоснежные и темные шары, при этом, в первой урне 2 белоснежных и 4 темных шара, во 2-ой — 3 белоснежных и 3 темных, в третьей — 4 белоснежных и 2 темных. Из одной из урн (непонятно из какой) наобум вытащат шар. Какова возможность того, что шар оказался белоснежным при условии, что он вытащат из первой урны?
Пусть событие А — вытаскивание белоснежного шара, а B — то, что он вытащат из первой урны. Из всех имеющихся шаров событию А способствует 9; из которых только 2 способствуют событию B. Таким образом рА(В) = 2/9.