Вероятность какого-либо одного из двух исходов независимых и несовместных событий равна сумме их вероятностей.

К примеру, какова возможность вытащить красноватый либо зеленоватый шар в рассмотренном выше примере? р(А)= 5/10, р(В) = 3/10, как следует, р(А v B) = 8/10.

Формулу (А.5) просто обобщить на случайное число подходящих исходов. Пусть из п несовместных событий k являются подходящими финалами, при этом, вероятности каждого составляют р₁, р₂,…, p_k. Тогда возможность пришествия хоть какого (хотя бы 1-го) из подходящих событий будет равна

Из соотношения (А.6) условия нормировки вероятностей (А.2) просто вывести два следствия:

Следствие 1. Если полное количество всех вероятных исходов равно п с вероятностями p₁,…, р_n, то

так как возникновение хоть какого-то из исходов достоверно. Это выражение можно считать обобщением условия нормировки.

Следствие 2. Если вероятных исходов всего два (А либо B), то пришествие 1-го значит не пришествие второго. Потому хоть какой из их является обратным другому (записывается В = ; читается «не А»). Так как р(А) + р(В) = 1, то р(B) = 1 — р(А) либо

К примеру, если обусловили ранее (пример А.2), что возможность вынуть красноватый либо зеленоватый шар составляет 8/10, то это значит, что возможность не вынуть хоть какой из их будет приравниваться 1 — 8/10 = 2/10.

Умножение вероятностей независящих совместных событий. Пусть событие А реализуется т₁ методами из п₁ равновероятных исходов 1-го опыта, а событие В — т₂ методами из п₂ равновероятных исходов другого опыта, независящего от первого. Спрашивается, какова возможность одновременного пришествия обоих событий (либо сложного действия С, состоящего в пришествии и А и B)? Другими словами желаем найти возможность совместного действия С = (А и B)*. Нередко С именуют произведением событий А и B. Так как каждому из п₁ исходов первого опыта соответствует п₂ исходов второго, то полное количество вероятных равновероятных исходов, разумеется, становится равным п₁∙п₂. Из их подходящими окажутся т₁∙т₂ исходов. Как следует, возможность совместного действия оказывается равной:

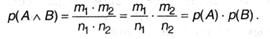
* Используя формализм математической логики можно записать С = А ^ B.