Попробуем выстроить обобщенную формулу для вероятности суммарного действия (А.5) на ситуацию, когда отдельные действия А и В возможно окажутся совместными, т.е. произойти сразу. В данном случае p(A v B) ≠ p(A) + p(B). Вправду: пусть как и раньше событие А производится при т1 из п равновероятных исходов опыта, а событие В — при m2 из числа тех же п вероятных исходов. Но из-за того, что может быть совместное пришествие А и В, финалы m1 и т2 окажутся не стопроцентно разными, т.е. посреди их могут быть одни и те же. Тогда суммарное количество подходящих исходов т ≤ т1 + т2 и, как следует, p(A v B) ≤ р(А) + р(В).
Пусть посреди т1 и т2 имеются т’ общих исходов; разумеется, это те случаи, когда А и В наступают сразу. Как следует, возможность совместного действия:
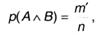
а полное количество разных подходящих исходов оказывается равным т = т1 + т2 — т’. Тогда возможность
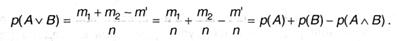
Совсем:
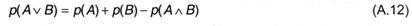
Таким образом, при определении вероятности суммы 2-ух событий (A v B) в общем случае требуется отыскивать и возможность их произведения (А ^ В). Это нетрудно сделать, если действия А и В независимы — в данном случае можно пользоваться формулой (А.9), подстановка которой в (А. 12) дает:
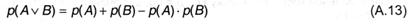
Просто созидать, что (А.5) оказывается личным случаем (А. 12) при условии несовместности А и B — тогда р(А ^ В) = 0.