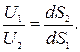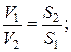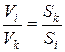Рассмотрим элементарную струйку (рис. 3.3), условно разделенную на отсеки сечениями 1-1, 2-2, 3-3, 4-4. Сечения проведены на расстояниях U₁, U₂, U₃, где U_1, U₂, U₃ – скорости движения жидкости в сечениях 1-1, 2-2, 3-3. В отсек 1-2 через сечение 1-1 площадью dS₁ со скоростью U₁ за одну секунду вольется объемное количество жидкости U₁ ∙dS₁., то есть расход жидкости через первое сечение dQ₁ = U₁ ∙dS₁.

Из этого же отсека за единицу времени через сечение 2-2 выльется количество жидкости Q₂ = U₂ ∙dS₂. Причем форма отсека 1-2 не изменилась, а его боковая поверхность непроницаема. Поэтому объем жидкости поступающей в отсек равен объему жидкости, которая из отсека вытекает:

U₁dS₁ = U₂dS₂. (3.7)

Аналогично по всем отсекам:

U₁ dS₁ = U₂ dS₂ = U₃ dS₃ = …. = U_іdS_і = const = dQ. (3.8)

Уравнение (3.8) является уравнением неразрывности элементарной струйки, которое показывает, что расход жидкости через любое сечение струйки величина постоянная, а струйка неразрывна, так как скорость жидкости не может быть равной нулю при положительном значении dQ. Из уравнения можно получить пропорции для любой пары сечений:

 (3.9)

Скорости жидкости в произвольной паре сечений обратно пропорциональны площади этих сечений. Для того, чтобы перейти от уравнения неразрывности струйки к уравнению неразрывности потока необходимо проинтегрировать уравнения неразрывности струйки в каждом сечении по площади сечения:

. (3.10)

Применяя понятие средней скорости потока в каждом сечении потока можно записать:

Q= V₁ S₁= V₂ S₂= …= V_іS_і = const,(3.11)

где V₁ V_2…. V_і – средние скорости жидкости в соответствующих сечениях;

S₁ S_2… S_і – площади сечений.

Уравнение (3.11) является уравнением неразрывности потока жидкости при установившемся движении. Анализируя уравнение легко установить, что любое изменение площади сечения приводит к изменению скорости в этом сечении.

Для потока также можно составить пары пропорций для любых сечений, например:

. (3.12)