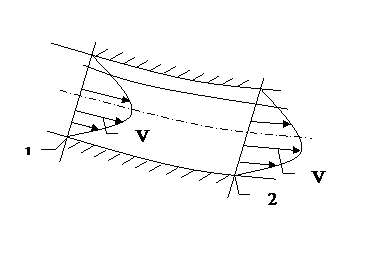
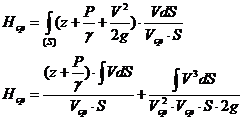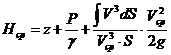Рис. 3.3

Будем считать, что по всему поперечному сечению . Строго говоря это утверждение справедливо только для параллельных трубок тока. Выделим в общем потоке элементарную струйку, такую тонкую, что изменением параметров в поперечном сечении будем пренебрегать. От трубки к трубке параметры потока будем считать переменными.

Введем понятие элементарной мощности потока, которая переносится элементарной струйкой dN.

Известно, что , тогда ; Учитывая, что 

Получим , но , а ; где Q – объемный расход жидкости, а γ – удельный вес. Тогда , .
Мощность всего потока определится как: 

Пользуясь теоремой о среднем:

(3.1) 
;
;

Подставляя в (3.1), получим:

(3.2) 

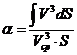  — коэффициент неравномерности потока. (3.3)

Экспериментально установлено следующее (3.4):

Δhi – суммарные потери полного напора в канале между сечениями 1 и 2.

Уравнение (3.4) – это уравнение Бернулли для реальной вязкой жидкости. Развернутая форма уравнения Бернулли: 

в каждом сечении мы должны найти среднее значение V и значение коэффициента неравномерности потока а.