Гидростатическое давление. Как известно, в покоящейся жидкости возможен лишь один вид напряжений – напряжения сжатия, т. е. гидростатическое давление. Гидростатическое давление в жидкости имеет следующие два свойства:
- На внешней поверхности гидростатическое давление всегда направлено по нормали, внутрь рассматриваемого объема жидкости.
Это свойство непосредственно вытекает из определения давления как напряжения от нормальной сжимающей силы. Под внешней поверхностью жидкости понимают не только поверхности раздела жидкости с газообразной средой или твердыми стенками, но и поверхности элементарных объемов, мысленно выделяемых из общего объема жидкости.
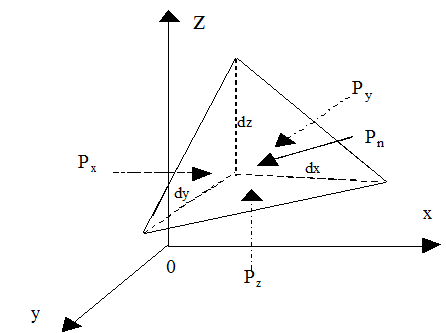
- В любой точке внутри жидкости гидростатическое давление по всем направлениям одинаково, т. е. давление не зависит от угла наклона площадки, на которую оно действует в данной точке. Для доказательства этого свойства выделим в неподвижной жидкости элементарный объем в форме прямоугольного тетраэдра с ребрами, параллельными координатным осям и соответственно равными dx, dy и dz ( рис. 2.1).
Рис. 2.1
Пусть на выделенный объем жидкости действует единичная массовая сила, составляющие которой равны X,Y и Z. Обозначим через px гидростатическое давление, действующее на грань, нормальную к оси 0x, через py давление, действующее на грань, нормальную к оси 0y, и т. д.
Гидростатическое давление, действующее на наклонную грань, обозначим через pn, а площадь этой грани – через dS. Все эти давления направлены по нормалям к соответствующим площадкам.
Составим уравнения равновесия выделенного объема жидкости сначала в направлении оси 0x.
Проекция сил давления на ось 0x равна:
![]()
Масса тетраэдра равна произведению его объема на плотность, т. е. ![]() , следовательно, массовая сила, действующая на тетраэдр вдоль оси 0x, равна:
, следовательно, массовая сила, действующая на тетраэдр вдоль оси 0x, равна:
![]()
Уравнения равновесия тетраэдра запишем в следующем виде:
![]()
Разделим это уравнение почленно на площадь ![]() , которая равна площади проекции наклонной грани dS на плоскость y0z, и, следовательно:
, которая равна площади проекции наклонной грани dS на плоскость y0z, и, следовательно:
Будем иметь:
![]()
При стремлении размеров тетраэдра к нулю последний член уравнения, содержащий множитель dx, будет также стремиться к нулю, а давления px и pn будут оставаться конечными величинами. Следовательно, в пределе получим, что px — pn =0 или px = pn. Аналогично составляя уравнения равновесия вдоль осей 0y и 0z, после таких же рассуждений получим, что py = pn, pz = pn, т. е.
px = py = pz = pn (2.1)
Так как размеры тетраэдра dx, dy и dz были взяты произвольно, то и наклон площадки dS произволен, и, следовательно, в пределе при стягивании тетраэдра в точку давление в этой точке по всем направлениям будет одинаково. Рассмотренное свойство давления в неподвижной жидкости имеет место также при движении идеальной жидкости. При движении же реальной жидкости возникают касательные напряжения, вследствие чего давление в реальной жидкости указанным свойством, строго говоря, не обладает.