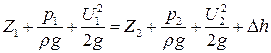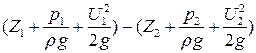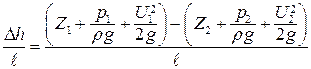При принятии большинства решений инженеру необходимо иметь дело с реальными вязкими жидкостями, что заставляет внести определенные коррективы в уравнения связанные с идеальной жидкостью. Наличие вязкости при движении жидкости вызывает появление трения, что приводит к потере части энергии, которой заряжена жидкость.

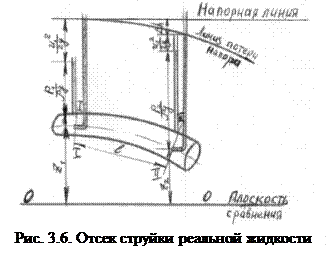
Рассмотрим отсек элементарной струйки реальной жидкости между сечениями 1-1 и 2-2. (рис.3.6). Сечения расположены на высоте z₁ и z₂ над плоскостью сравнения 0-0 Трубки Пито расположенные в этих сечениях показали: 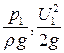 и .

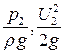Если бы жидкость была идеальной, суммы высот в этих сечениях (z₁+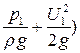и (z₂+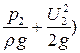были бы равны. В действительности это не так, и сумма показаний второй трубки будет меньше на ∆h – потерю напора.

Величина ∆h называется потерей напора на расстоянии между сечениями. Линия полного гидродинамического напора расположится с наклоном. Уравнение Бернулли для сечений 1-1 и 2-2 элементарной струйки реальной жидкости будет иметь вид:

. (3.20)

Отсюда

∆h = . (3.21)

Если помножить каждый член уравнения на g (возвращаясь к энергетической трактовке уравнения Бернулли (3.17)), то становится понятным, что в связи с наличием трения жидкость теряет при движении часть энергии g∆h. В различных написаниях уравнения Бернулли эта частичка имеет различное название (потеря напора, потеря давления) но физическая суть процесса остается неизменной – жидкость теряет часть энергии.

Падение напорной линии (линии полного гидродинамического напора) в направлении движения характеризуется гидравлическим уклоном:

J =, (3.22)

где l – расстояние между сечениями 1-1 и 2-2.