Пример 1

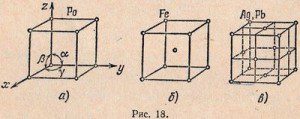
Зная, что микрокристаллы серебра имеют кубическую гранецентрированную решетку (рис. 18, в), определить число ближайших «соседей» каждого атома серебра; число атомов, приходящихся на элементарную ячейку решетки; постоянную решетки; наименьшее расстояние между частицами.

Дано: μ=107,88*10^-3 кг/моль — молярная масса серебра, р=1,05*10⁴ кг/м³ — плотность серебра, N_A=6,023*10²³ моль^-1 — постоянная Авогадро.

Найти: α — постоянную решетки; d — наименьшее расстояние между частицами.

Решение. Если взять атом в одной из вершин куба, то в каждой из взаимно перпендикулярных плоскостей у него окажется 4 соседа-атома в центрах граней. Всего соседей будет 12.

На элементарную ячейку приходится по одному атому из расположенных в вершине куба и по три — из расположенных в центрах его граней — всего 4 атома.

Параметры кубической решетки определяются по формулам:

где k—число атомов в элементарной ячейке, q=1 —число атомов (ионов) в молекуле. Для ионных решеток NaСl, ZnQ q=2.

Подставляя в полученные выражения числовые значения физических величин, получаем:

Ответ. Постоянная решетки примерно равна 4,09*10^-10 м; наименьшее расстояние между атомами 2,89*10^-10 м.

Пример 2

К. п. д. холодильника 80%. Какое количество холодильного агента (фреона-12) должно испариться для обращения в лед 150 г воды с начальной температурой 289К?

Дано: η=0,80 — к. п. д. холодильника, m_B=0,150 кг — масса охлаждаемой воды, Т₁=289К — начальная температура воды, Т₂=273К — температура плавления льда, λ=3,32*10⁵ Дж/кг — удельная теплота плавления льда, r_Ф=1,68*10⁶ Дж/кг — удельная теплота испарения фреона.

Найти: m_Ф—массу испарившегося фреона.

Решение. Задача решается с помощью уравнения теплового баланса. Количество тепла, которое отдает вода при охлаждении и замерзании:

Q₁=c_Bm_B(T₁-T₂)+λm_B

Количество тепла, затраченное на испарение фреона:

Q=r_Фm_Ф

Количества тепла Q₁ и Q связаны между собой формулой:

η=Q₁/Q

На основании закона сохранения энергии составляем уравнение теплового баланса:

c_Bm_B(T₁-T₂)+λm_B= r_Фm_Фη

Решив уравнение теплового баланса относительно m_Ф, найдем:

Подставляя числовые значения, получаем:

Ответ. Масса испарившегося фреона примерно равна 0,044 кг.