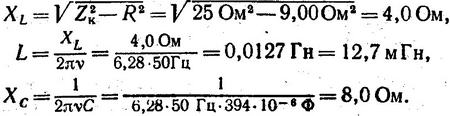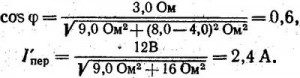Пример
В рамке, содержащей 100 витков и равномерно вращающейся в однородном магнитном поле, поток магнитной индукции изменяется по закону Ф=2,0*10-3 cos 314t [Вб]. Определить: зависимость возникающей в рамке э. д. с. от времени; максимальное и действующее значения э. д. с.; мгновенное значение э. д. с. для t=0,0050 с. Как изменится зависимость э. д. с. от времени при увеличении угловой скорости вращения рамки в два раза?
Дано: N=100 — число витков в рамке; Ф=2,0*10-3cos314t [Вб] — зависимость магнитного потока в рамке от времени, t=0,0050 с — момент времени, для которого определяется мгновенное значение э.д.с.
Найти: е=f(t) — зависимость возникающей в рамке э. д. с. от времени; Ԑ0 —максимальное значение э. д. с.; Ԑ — действующее значение э. д. с.; е — мгновенное значение э. д. с. для t=0,0050 с; e1=f(t) — зависимость э. д. с. от времени при увеличении угловой скорости рамки в два раза.
Решение. Мгновенное значение э. д. с., возникающей в каждом витке, равно первой производной от магнитного потока по времени, взятой со знаком минус, т. е. е= — Фt‘ . При N витках е=—NФt‘. Так как Ф=Ф0 соs ωt, то:
Находим зависимость мгновенного значения э. д. с. от времени:
Максимальное значение э. д. с.
Действующее значение э. д. с.
Мгновенное значение э. д. с. найдем, подставив в уравнение е= Ԑ0 sin ωt соответствующее значение t. Вычислим мгновенную э. д. с. для t=0,0050 с:
Из формулы е=NωФ0sinωt видно, что при увеличении ω в два раза максимальное значение э. д. с. и циклическая частота изменения э. д. с. возрастают в два раза. Мгновенное значение э. д. с. определяется при этом по формуле:
где ω — первоначальное значение угловой скорости вращения рамки. Находим зависимость e1=f(t) при увеличении угловой скорости в два раза:
Ответ. Зависимость э. д. с. возникающей в рамке, от времени определяется формулой е=62,8sin314t [В]; максимальное значение э. д. с. Ԑ0=62,8 В; действующее значение э. д. с. Ԑ≈44,5 В; мгновенное значение э. д. с. для t=0,0050 c равно 62,8 В. При увеличении угловой скорости вращения рамки в два раза мгновенное значение э. д. с. определяется по формуле e1 = 125,6 sin 628t.
Пример
Сколько пар магнитных полюсов имеет ротор гидрогенератора, совершающего 120 об/мин, если гидрогенератор вырабатывает переменный ток стандартной частоты?
Дано: n=120 об/мин — число оборотов ротора в минуту, v=50 Гц — стандартная частота переменного тока.
Найти: р — число пар магнитных полюсов.
Решение. Частота переменного тока v связана с частотой вращения ротора генератора vмex зависимостью v=pvмex.
Выражая частоту вращения ротора генератора в об/с, окончательно получим:
Ответ. Ротор гидрогенератора имеет 25 пар магнитных полюсов.
Пример
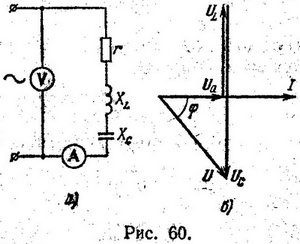
При включении катушки в цепь постоянного тока с напряжением 12 В амперметр показал силу тока 4,0 А. При включении той же катушки в цепь переменного тока с частотой 50 Гц и напряжением, 12 В амперметр показал ток 2,4 А. Определить индуктивность катушки. Чему будет равна активная мощность тока в цепи, если последовательно с катушкой включить конденсатор емкостью 394 мкФ (рис. 60, а)? Нарисовать векторную диаграмму для этого случая.
Дано: Uпос=12 В—напряжение постоянного тока, Iпос= 4,0 A—сила постоянного тока, Uпер=12 В—напряжение переменного тока, Iпер=2,4 А—сила переменного тока, v =50 Гц—частота переменного тока, С=394*10-6Ф—электроемкость конденсатора.
Найти: L — индуктивность катушки; Р — активную мощность тока.
Решение. Так как яри постоянном токе реактивные сопротивления отсутствуют, то в этом случае по закону Ома можно найти активное сопротивление катушки R=Uпос/Iпос. При переменном токе с помощью того же закона можно найти полное сопротивление катушки Zк=Uпер/Iпер, а затем определить XL из формулы Zк2 = R2 + XL2. Зная XL и частоту тока v и учитывая, что XL= ωL= 2πvL, найдем L.
Находим активное сопротивление катушки:
Ищем полное сопротивление катушки:
Определяем XL и L катушки, а также сопротивление конденсатора ХC:
Активную мощность тока при включенном в цепь конденсаторе можно рассчитать из формулы:
где I’пер определяется соотношением
![]()
Нужный для вычисления коэффициент мощности определяется следующим образом:
Подставляя числовые значения, получаем:
Следовательно,
Р=12 В*2,4 А*0,6=17,3 Вт
Так как Хс больше ХL, то в данном случае вектор напряжения будет отставать от вектора тока на угол φ. Учитывая, что UС вдвое больше UL строим векторную диаграмму (рис. 60, б).
Ответ. Индуктивность катушки 12,7 мГн, активная мощность тока при последовательном соединении катушки и конденсатора 17,3 Вт.