Классификация движения
Гидродинамика изучает законы движения жидкостей. Движение жидкости характеризуется скоростью частиц жидкости в отдельных точках потока, давлением возникающим в этих точках и формой потока. Поэтому основная задача гидродинамики – определения этих величин в различных условиях движения. Как скорость ui, так и давление рi в этой точке зависят от координат и от времени. Поэтому, можно записать:
u = f1 (x, y, z, τ). (3.1)
р = f2 (x, y, z, τ).
Во многих процессах параметры не зависят от времени и тогда:
u = f1 (x, y, z). (3.2)
р = f2 (x, y, z).
В первом случае, когда поток меняется во времени, движение называется неустановившимся, во втором – скорость и давление в данной точке являются величинами постоянными и не зависящими от времени, в потоке они зависят только от координат, а движение называется установившимся. Иногда такой поток называют стационарным. Установившееся движение подразделяют на равномерное и неравномерное. Равномерным называется такой вид установившегося движения, при котором форма потока не меняется по длине потока.
В зависимости от причин, которые вызывают движение, отличают напорное и безнапорное движение. Их также называют вынужденным и естественным. Напорное движение возникает под действием разности давлений по длине потока создаваемой искусственно (насосом, компрессором, вентилятором и т.д.) При напорном движении жидкость заполняет всё сечение трубы полностью, такой тип движения чаще присущ закрытым системам.
При безнапорном естественном движении движущей силой является сила тяжести. Такое движение осуществляется обычно со свободной поверхностью жидкости. В большинстве случаев свободная поверхность сообщается с атмосферой и поэтому давление на поверхности потока – атмосферное.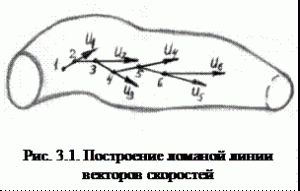
Решение многих задач гидродинамики базируется на допущении о струйчатом характере потока, то есть, что поток состоит из отдельных элементарных струек, не изменяющих своей формы. Дадим определение понятию элементарной струйки. Рассмотрим установившееся движение потока жидкости. Выберем в потоке произвольную точку 1 и построим вектор скорости из этой точки u1. На этом векторе на бесконечно малом расстоянии от точки 1 выберем точку 2 и построим вектор скорости u2. На этом векторе на бесконечно малом расстоянии от точки 2 выберем точку 3 и построим очередной вектор скорости u3.
И так далее. Уменьшая до нуля расстояние между точками вместо ломаной кривой 1-2-3, мы получим плавную кривую линию тока. Линией тока называется такая кривая, к каждой точке которой в данный момент времени
вектор скорости является касательным. При установившемся движении линия тока совпадает с траекторией частицы жидкости. Построим вокруг точки 1 замкнутый контур, который ограничивает элементарную площадку dS. Через все наружные точки контура проведем линии тока и получим полую трубку тока. Теперь заполним полую трубку линиями тока, и получим элементарную струйку.
Базируясь на понятиях, использованных при построении элементарной струйки, сформулируем свойства элементарной струйки при установившемся движении:
- Форма элементарной струйки неизменна.
- Поверхность элементарной струйки непроницаема.
- Скорость в любой точке поперечного сечения струйки одинакова.
Поток жидкости, состоящий из элементарных струек, обладающих вышеперечисленными свойствами, называется струйчатой моделью движения жидкости.