После того, как подверглись рассмотрению вероятные методы записи алгоритмов, полностью закономерным представляется вопрос о технологии их разработки. До середины 60-х годов теории разработки алгоритмов не было — процесс разработки полностью определялся опытом и искусством программера. Но по мере роста трудности программ появилась необходимость сотворения методологии их разработки, и она появилась в виде структурного программирования. Идеи структурного программирования были высказаны в 1965 г. Э. Дейкстрой, но сведены в некоторую законченную систему правил они не были. В том же году итальянские арифметики К. Бом и Д. Джакопини определили аксиому о структурности. До этого, чем разглядеть ее сущность, нужно ввести некие понятия.
Так как метод определяет порядок обработки инфы, он должен содержать, с одной стороны, деяния по обработке, а с другой стороны, порядок их следования, именуемым потоком управления.
Рассмотренные выше блоки, связанные с обработкой данных, делятся на обыкновенные и условные. Особенность обычного деяния в том, что оно имеет один вход и один выход, в отличии от условного, владеющим 2-мя выходами зависимо от того, настоящим ли окажется условие. Обычное действие не значит, что оно единственное — это может быть некая последовательность действий.
Часть метода, организованная как обычное действие, т.е. имеющая один вход (выполнение начинается всегда с 1-го и такого же деяния) и один выход (т.е. после окончания данного блока всегда начинает производиться одно и то же действие), именуется многофункциональным блоком.
Из этого определения, а именно, следует, что каждое обычное действие является многофункциональным блоком, а условное — нет.
Согласно положениям структурного программирования можно выделить всего три разных варианта организации потока управления действиями метода. Поток управления может владеть последующими качествами:
- каждый блок производится менее 1-го раза;
- производится каждый блок.
Поток управления, в каком производятся оба эти характеристики, именуется линейным — в нем несколько многофункциональных блоков производятся поочередно. Линейному сгустку на языке блок-схем соответствует структура:

Разумеется несколько блоков, связанных линейным потоком управления, могут быть объединены в один многофункциональный блок:

2-ой тип потока управления именуется ветвлением — он организует выполнение 1-го из 2-ух многофункциональных блоков зависимо от значения проверяемого логического условия. Блок-схема структуры:
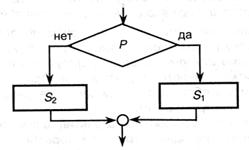
В этом типе производится свойство (1), свойство (2) — нет. Если структура содержит два многофункциональных блока (S1 и S2), ветвление именуется полным; может быть существование неполного ветвления — при всем этом один из блоков пуст (обычно S2).
3-ий тип потока управления именуется повторяющимся — он организует неоднократное повторение многофункционального блока, пока логическое условие его выполнение является настоящим. Для повторяющегося потока производится свойство (2), но не производится (1). Его блок-схема показана на рисунке.
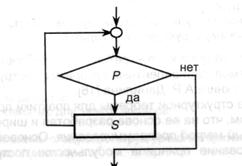
Так как ветвление и повторяющийся типы управления имеют один вход и один выход, они в целом также подходят под определение многофункционального блока. Введем рекурсивным образом понятие стандартного многофункционального блока:
- каждое обычное действие есть стандартный многофункциональный блок;
- любая из обрисованных 3-х управляющих структур является стандартным многофункциональным блоком, если все входящие в их блоки являются стандартными многофункциональными;
- других стандартных многофункциональных блоков не существует.
Определим очередное понятие:
Метод именуется структурным, если он может быть представлен стандартным многофункциональным блоком.
Другими словами, структурный метод представляет собой комбинацию 3-х рассмотренных выше структур (время от времени они именуются базисными алгоритмическими структурами). Непременно, не все методы являются структурными. Но конкретно структурные методы владеют рядом восхитительных преимуществ по сопоставлению с неструктурными:
- понятность и простота восприятия метода (так как невелико число начальных структур, которыми он образован);
- проверяемость (для проверки хоть какой из главных структур довольно убедиться в корректности входящих в нее многофункциональных блоков);
- модифицируемость (она состоит в простоте конфигурации структуры метода, так как составляющие блоки относительно независимы).
После введенных определений можно сконструировать структурную аксиому Бома-Джакопини: