Комбинационные схемы, хотя и позволяют воплотить любые фиксированные зависимости меж входными и выходными сигналами, не могут изменять нрава собственного поведения (т.е. последовательности обработки данных) — хоть какое такое изменение просит конфигурации структуры схемы, т.е., на самом деле, переходу к другой схеме. Решить делему перестройки работы без конфигурации структуры схемы может быть, если ввести в нее элементы памяти, которые позволяли бы фиксировать и сохранять промежные состояния устройства — в данном случае выходной сигнал будет зависеть не только лишь от входного сигнала, да и от состояния схемы. Если количество таких частей естественно, то, как указывалось выше, дискретное устройство будет называться конечным автоматом.
Конечным автоматом именуется система <X, Y, Q, Y, Q>, в какой X и Y являются конечными входным и выходным алфавитами, Q — конечным обилием внутренних состояний, Y(x, q) — функцией переходов и Q(x,q) — функцией выходов.
Как указывалось ранее, Y(x,q) задает порядок преобразования входных знаков и состояния автомата на прошлом такте в состояние на следующем, a Q(x,q) — преобразования входных знаков и состояния автомата на текущем такте в выходной знак. Если q0 — изначальное состояние автомата, а i — номер такта, то его работа описывается системой:
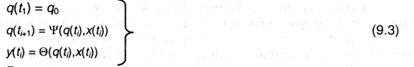
Данные соотношения получили заглавие системы канонических уравнений конечного автомата. Пользуясь ими можно, начиная с q0, поочередно отыскивать все следующие состояния автомата и выходные знаки.
Выделяются два типа автоматов — инициальные и неинициальные. В инициальных автоматах изначальное состояние фиксировано (т.е. они всегда начинают работать из 1-го и такого же состояния q0). В неинициальных автоматах в качестве исходного состояния может быть выбрано хоть какое из огромного количества Q; этим выбором определяется предстоящее поведение автомата.
Представление определенного конечного автомата практически сводится к описанию задающих его автоматных функций. Из системы (9.3) следует, что при конечном числе вероятных внутренних состояний количество вероятных значений автоматных функции также оказывается конечным. Их описание может быть разными методами, более всераспространенными из которых является табличный и при помощи диаграмм.
В табличном методе автоматные функции задаются 2-мя конечными таблицами, называемыми соответственно матрицей переходов и матрицей выходов. В этих таблицах строчки обозначаются знаками входного алфавита, а столбцы — знаками внутреннего алфавита (знаками, кодирующими внутреннее состояние автомата). В матрице переходов на скрещении строчки (xk) и столбца (qr) помещаются значения функции Y (qr, xk), а в матрице выходов — значения функции Q(qr, xk).