Начнем с неких общих замечаний относительно понятия число. Можно считать, что хоть какое число имеет значение (содержание) и форму представления*. Значение числа задает его отношение к значениям других чисел («больше», «меньше», «равно») и, как следует, порядок расположения чисел на числовой оси. Форма представления, как надо из наименования, определяет порядок записи числа при помощи созданных для этого символов. При всем этом значение числа является инвариантом, т.е. не находится в зависимости от метода его представления. Это значит также, что число с одним и этим же значением может быть записано по-разному, т.е. отсутствует взаимно однозначное соответствие меж представлением числа и его значением. В связи с этим появляются вопросы, во-1-х, о формах представления чисел, и, во-2-х, о способности и методах перехода от одной формы к другой.

* Ситуация очень припоминает порядок внедрением переменных в программках — они тоже имеют значение и имя. Эта аналогия подчеркивает общность подхода к представлению данных независимо от того, кому (либо чему) эти данные предусмотрены.

Метод представления числа определяется системой счисления.

Система счисления — это правило записи чисел при помощи данного набора особых символов — цифр.

Людьми использовались разные методы записи чисел, которые можно соединить в несколько групп: унарная, непозиционные и позиционные.

Унарная — это система счисления, в какой для записи чисел употребляется только один символ — | («палочка»). Последующее число выходит из предшествующего добавлением новейшей |; их количество (сумма) равно самому числу. Конкретно такая система применяется для исходного обучения счету малышей (можно вспомнить «счетные палочки»); внедрение унарной системы оказывается принципиальным педагогическим приемом для введения малышей в мир чисел и действий с ними. Но, как увидим в предстоящем, унарная система принципиальна также в теоретическом отношении, так как в ней число представляется более обычным методом и, как следует, ординарны операции с ним. Не считая того, конкретно унарная система определяет значение целого числа количеством содержащихся в нем единиц, которое, как было сказано, не находится в зависимости от формы представления. Для записи числа в унарной системе в предстоящем будем использовать обозначение Z₁.

Из непозиционных более всераспространенной можно считать римскую систему счисления. В ней некие базисные числа обозначены большими латинскими знаками: 1 — I, 5 — V, 10 — Х, 50 — L , 100 — С, 500 — D, 1000 — М. Все другие числа строятся композиций базисных в согласовании со последующими правилами:

• если цифра наименьшего значения стоит справа от большей числа, то их значения суммируются; если слева — то наименьшее значение вычитается из большего.
• числа I, X, С и М могут следовать попорядку менее 3-х раз любая;
• числа V, L и D могут употребляться в записи числа менее 1-го раза.

К примеру, запись XIX соответствует числу 19, MDXLIX — числу 1549. Запись чисел в таковой системе громоздка и неудобна, но еще больше неловким оказывается выполнение в ней даже самых обычных арифметических операций. Отсутствие нуля и символов для чисел больше М не позволяют римскими цифрами записать хоть какое число (хотя бы натуральное). По обозначенным причинам сейчас римская система употребляется только для нумерации.

В текущее время для представления чисел используют, в главном, позиционные системы счисления.

Позиционными именуются системы счисления, в каких значение каждой числа в изображении числа определяется ее положением (позицией) в ряду других цифр.

Более всераспространенной и обычной является система счисления, в какой для записи чисел употребляется 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Число представляет собой короткую запись многочлена, в который входят степени некого другого числа — основания системы счисления. К примеру,

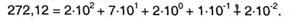
В данном числе цифра 2 встречается три раза, но, значение этих цифр различно и определяется их положением (позицией) в числе. Количество цифр для построения чисел, разумеется, равно основанию системы счисления. Также разумеется, что наибольшая цифра на 1 меньше основания. Причина широкого распространения конкретно десятичной системы счисления понятна — она происходит от унарной системы с пальцами рук в качестве «палочек». Но в истории населения земли имеются свидетельства использования и других систем счисления — пятиричной, шестиричной, двенадцатиричной, двадцатиричной и даже шестидесятиричной — об этом можно прочесть, к примеру, в книжке С.В. Фомина [43].

Общим для унарной и римской систем счисления будет то, что значение числа в их определяется средством операций сложения и вычитания базовых цифр, из которых составлено число, независимо от их позиции в числе. Такие системы получили заглавие аддитивных. В отличие от их позиционное представление следует считать аддитивно-мультипликативным, так как значение числа определяется операциями умножения и сложения. Главной же особенностью позиционного представления будет то, что в нем средством конечного набора символов (цифр, разделителя десятичных разрядов и обозначения знака числа) можно записать огромное количество разных чисел. Не считая того, в позиционных системах еще легче, чем в аддитивных, осуществляются операции умножения и деления. Конкретно эти происшествия обуславливают преобладание позиционных систем при обработке чисел как человеком, так и компом.

По принципу, положенному в базу десятичной системы счисления, разумеется, можно выстроить системы с другим основанием. Пусть р — основание системы счисления. Тогда хоть какое число Z (пока ограничимся только целыми числами), удовлетворяющее условию Z < p^k (k ≥ 0, целое), может быть представлено в виде многочлена со степенями р (при всем этом, разумеется, наибольший показатель степени будет равен k — 1):

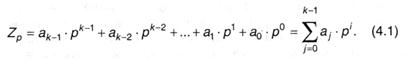
Из коэффициентов a_j при степенях основания строится сокращенная запись числа:

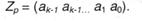
Индекс р у числа Z показывает, что оно записано в системе счисления с основанием р; общее число цифр числа равно k. Все коэффициенты a_j — целые числа, удовлетворяющие условию:

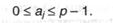
Уместно задаться вопросом: каково малое значение р? р = 1 нереально, так как тогда все a_j = 0 и форма (4.1) теряет смысл. 1-ое допустимое значение р = 2 — оно и является наименьшим для позиционных систем. Система счисления с основанием 2 именуется двоичной. Цифрами двоичной системы являются 0 и 1, а форма (4.1) строится по степеням 2. Энтузиазм конкретно к этой системе счисления связан с тем, что, как указывалось выше, неважно какая информация в компьютерах представляется при помощи 2-ух состояний — 0 и 1, которые просто реализуются на техническом уровне. Вместе с двоичной в компьютерах употребляются 8-ричная и 16-ричная системы счисления — предпосылки подвергнутся рассмотрению дальше.

Нужно снова выделить, что значение целого числа, т.е. полное количество входящих в него единиц, не находится в зависимости от метода его представления и остается схожим во всех системах счисления; различаются только формы представления 1-го и такого же количественного содержания числа.