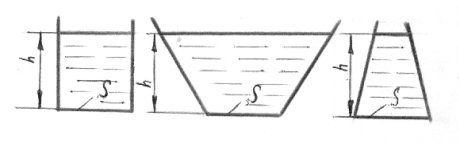
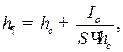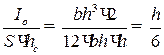Определим силу давления жидкости на дно сосуда. Предположим, что имеются три сосуда разной формы с плоскими днищами одинаковой площади (рис. 2.9). Уровни воды, налитой в эти сосуды, одинаковы.

Рис. 2.9. Гидростатический парадокс

Тогда силу давления, действующего на дно сосудов, можно определить Оказывается, что сила давления на плоское горизонтальное дно зависит не от формы сосуда, а только от площади дна и высоты уровня жидкости над этим дном. Это положение носит название гидростатического парадокса, потому что при наличии разного количества жидкости в сосудах, сила давления на дно в этих трех сосудах будет одинакова.

Для определения силы давления жидкости на плоскую стенку, произвольно ориентированную в жидкости (рис. 2.10), следует умножить значение площади стенки на гидростатическое давление в точке центра тяжести стенки. Сила избыточного давления, создаваемого жидкостью – это вес столба жидкости, основанием которого является площадь стенки, а высотой – глубина погружения центра тяжести стенки (2.31):

где h_с – глубина погружения центра тяжести стенки;

S – площадь стенки.

Если над свободной поверхностью жидкости существует давление р₀, то сила давления будет определена (2.32):

Иногда при расчётах необходимо определить не только силу давления, но и точку приложения этой силы. Точка приложения силы гидростатического давления называется центром давления. Сила давления, в отличие от силы тяжести, увеличивается с глубиной погружения, и поэтому центр давления будет лежать ниже центра тяжести. Центр давления совпадает с центром тяжести только при горизонтальном расположении плоской фигуры, во всех остальных случаях произвольного расположения фигуры центр давления смещается ниже центра тяжести на расстояние: .

(2.33)

где 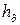– глубина погружения центра давления;

I₀ – момент инерции фигуры относительно горизонтальной оси, которая проходит через центр тяжести;

S – площадь плоской фигуры;

h_c – глубина погружения центра тяжести.

Для прямоугольных фигур глубину погружения центра давления можно принять равной 2/3 от полной высоты погруженной фигуры, так как момент инерции для прямоугольников , площадь прямоугольника S= b*h, а глубина погружения центра тяжести 

(2.34)