При разработке конечных автоматов употребляется несколько типов частей памяти, из которых основными следует считать элемент задержки, двоичный триггер и двоичный счетчик.
Элемент задержки имеет функцию перехода вида q(ti) = x(ti) и функцию выхода вида y(ti) = q(ti—1). Из их, а именно видно, что y(ti+1) = q(ti) = x(ti), т.е. элемент производит задержку входного сигнала на один такт (поданный на неком такте сигнал поступит на выход только на последующем такте). Задержка употребляется в линиях оборотной связи, когда, к примеру, сигнал подается с выхода схемы на ее вход.
Двоичный триггер имеет два входа х1 и х2. Функция переходов имеет последующий вид: q(ti) = Y (x1(ti), x2(ti)); ее значения инсталлируются таким образом: Y(1,0) = 1, т.е. при подаче 1 на вход х, и 0 на вход х2 триггер перебегает в состояние 1 и сохраняет это состояние до того времени, пока оно не будет заменено другим; Y(0,1) = 0, т.е. 0 на x1 и 1 на х2 переводят триггер в состояние 0; Yi(0, 0) = Yi—1, т.е. при обоих нулевых сигналах состояние триггера не меняется. Одновременная подача единичных сигналов на оба входа триггера исключается конструкцией схемы. Выходная функция триггера при всех состояниях у(ti) = q(ti), т.е. на выход подается текущее состояние триггера, но оно от этого не меняется. Таким образом, триггер сохраняет сколь угодно длительно записанный в него бит информации. Объединения схожих частей образуют регистры и ячейки памяти, из которых, в свою очередь, строится вся память устройства. Память эта по количеству двоичных частей, очевидно, конечна.
Двоичный счетчик имеет один вход; он меняет свое состояние на обратное, если на входе 1, и сохраняет его, если на входе 0. Разумеется, q(ti) = Y(x(ti), q(ti—1)), при этом, Y(1,1) = 0, Y(1,0) = 1, Y(0,1) = 1, Y(0,0) = 0; y(ti) = q(ti).
Добавлением частей памяти к базису из логических частей, использовавшихся при построении комбинационных схем, образует новый базис, который обладает свойством полноты. Под полнотой понимается возможность построения на базе данного базиса схемы, задающей хоть какое отображение последовательностей входных сигналов на последовательности выходных, которое вообщем может быть задано дискретным двоичным преобразователем информации с конечной памятью. Другими словами, может быть построение всех схем, поведение которых определяется как входными сигналами, так и их состоянием на прошлом такте.
Дальше будем рассматривать схемы с единственным видом памяти — задержкой (на схемах будет обозначаться Z). Схемы строятся по определенным правилам. Начальными понятиями являются: элемент (логический либо задержка) и вход в схему (он именуется полюсом). Можно дать последующее индуктивное определение схемы (попутно определяется понятие верхушки схемы):
- совокупность полюсов, соответственная некому набору входных переменных х1, … xn, является схемой; верхушками схемы будут ее полюсы;
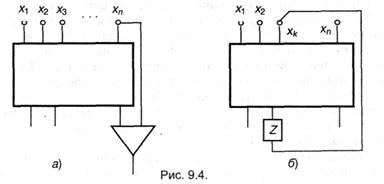
- итог присоединения к верхушкам схемы всех входов некого базового элемента есть схема; полюсами будут все полюсы начальной схемы, а верхушками — все верхушки начальной схемы и выход присоединенного элемента (рис. 9.4, а);
- итог присоединения выхода задержки к некому полюсу xk есть схема; ее полюсами будут все полюсы начальной схемы, кроме xk, a верхушками — все верхушки начальной схемы, не считая xk (рис. 9.4, б).
В согласовании с правилами построения схем каждой ее верхушке может быть сопоставлена функция, указывающая значение сигнала на неком такте ti, а каждой задержке Zj — дополнительная функция, указывающая ее состояние на данном такте qj(ti). Значения функций определяются по последующим правилам:
- полюсу хr приписывается дискретная функция xr(t), значения которой являются значениями t в такты 0, 1, 2, …;
- верхушке, соответственной выходу логического элемента (рис. 9.4, а), приписывается значение, сформированное этим элементом согласно сигналам на его входе;
- если элемент задержки Zj присоединен к верхушке, которой приписана некая функция f(t), то согласно значениям автоматных функций задержки для состояния задержки принимается qj(ti) = f(ti), а выходу задержки приписывается qj(ti—1);
- если задержка присоединяется к полюсу (рис. 9.4, б), то в функциях, приписываемых верхушкам и состояниям задержек, функция xk(ti) всюду заменяется на qj(ti—1).
Неважно какая верно построенная схема из логических частей и задержек обладает последующими 2-мя качествами:
- каждый вход всякого элемента присоединен или к полюсу, или к выходу другого элемента;
- в хоть какой повторяющейся цепочке частей находится по последней мере один элемент задержки.
В отношении схем, содержащих элементы памяти, решаются задачки анализа и синтеза. Задачка анализа заключается в том, чтоб по данной схеме отыскать реализуемый автомат, т.е. установить все алфавиты, также очевидный вид системы канонических уравнений. Задачка синтеза является оборотной по отношению к задачке анализа: по данному конечному автомату выстроить реализующую его схему над избранным базисом (логические элементы и элементы памяти). В базе анализа схем лежит способ устранения задержек. Его мысль заключается в том, что из схемы можно удалить имеющиеся задержки, заменив их дополнительными полюсами, на которые поданы сигналы, надлежащие значениям функции, приписываемые задержке. В итоге выходит новенькая схема только из логических частей с расширенным (по отношению к начальному) входным алфавитом. Для этой схемы строятся автоматные функции и, тем, устанавливается вид конечного автомата.