Выполнить преобразование Z₂ = 110001₂ → Z₈. Начальное число разбивается на группы по три разряда справа влево (8 = 2³, как следует, r = 3) и любая тройка в согласовании с таблицей 4.1. переводится в 8-ричную систему счисления независимо от других троек:

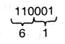
Как следует, 110001₂ = 61₈. Аналогично, разбивая Z₂ на группы по 4 двоичные числа и дополняя старшую группу незначащими нулями слева, получим 110001₂= 31₁₆.

Аксиома 2. Для преобразования целого числа Z_p → Z_q в этом случае, если системы счисления связаны соотношением р = q^r, где r — целое число большее 1, довольно каждую цифру Z_p поменять подходящим r-разрядным числом в системе счисления q, дополняя его по мере надобности незначащими нулями слева до группы в r цифр.

Подтверждение:

Пусть начальное число содержит две числа, т.е.

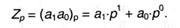
Для каждой числа справедливо: 0 ≤ a_i ≤ р — 1 и так как р = q_r, 0 ≤ a_i ≤ q^r-1, то в представлении этих цифр в системе счисления q наибольшая степень многочленов (4.1) будет менее r — 1 и эти многочлены будут содержать по r цифр:

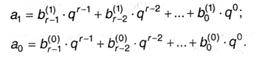
Тогда

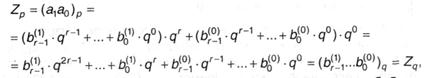
при этом, число Z_q содержит 2r цифр. Подтверждение просто обобщается на случай случайного количества цифр в числе Z_p.

Пример 4.7 Выполнить преобразование D3₁₆ → Z₂.

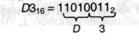
Переходы Z₈ → Z₁₆ и Z₁₆ → Z₈, разумеется, удобнее производить через промежуточный переход к двоичной системе. К примеру, 123₈ = 001010011₂ = 53₁₆.