Как отмечалось при рассмотрении начальных понятий информатики, для представления дискретных сообщений употребляется некий алфавит. Но однозначное соответствие меж содержащейся в сообщении информацией и его алфавитом отсутствует.

В целом ряде практических приложений появляется необходимость перевода сообщения хода из 1-го алфавита к другому, при этом, такое преобразование не должно приводить к потере инфы.

Введем ряд с определений.

Будем считать, что источник представляет информацию в форме дискретного сообщения, используя для этого алфавит, который в предстоящем условимся именовать первичным. Дальше это сообщение попадает в устройство, модифицирующее и представляющее его в другом алфавите — этот алфавит назовем вторичным.

Код — (1) правило, описывающее соответствие символов либо их сочетаний первичного алфавита знакам либо их сочетаниям вторичного алфавита. (2) набор символов вторичного алфавита, применяемый для представления символов либо их сочетаний первичного алфавита.

Кодирование — перевод инфы, представленной сообщением в первичном алфавите, в последовательность кодов.

Декодирование — операция, оборотная кодированию, т.е. восстановление инфы в первичном алфавите по приобретенной последовательности кодов.

Кодер — устройство, обеспечивающее выполнение операции кодировки.

Декодер — устройство, производящее декодирование.

Операции кодировки и декодирования именуются обратимыми, если их последовательное применение обеспечивает возврат к начальной инфы без каких-то ее утрат.

Примером обратимого кодировки является представление символов в телеграфном коде и их восстановление после передачи. Примером кодировки необратимого может служить перевод с 1-го естественного языка на другой — оборотный перевод, вообщем говоря, не восстанавливает начального текста. Непременно, для практических задач, связанных со знаковым представлением инфы, возможность восстановления инфы по ее коду является нужным условием внедрения кода, потому в предстоящем изложении ограничим себя рассмотрением только обратимого кодировки.

Кодирование предшествует передаче и хранению инфы. При всем этом, как указывалось ранее, хранение связано с фиксацией некого состояния носителя инфы, а передача — с конфигурацией состояния со временем (т.е. процессом). Эти состояния либо сигналы будем именовать простыми сигналами —конкретно их совокупа и составляет вторичный алфавит.

Не обсуждая технических сторон передачи и хранения сообщения (т.е. того, каким образом практически реализованы передача-прием последовательности сигналов либо фиксация состояний), попробуем дать математическую постановку задачки кодировки.

Пусть первичный алфавит А состоит из N символов со средней информацией на символ I^(A), а вторичный алфавит B — из М символов со средней информацией на символ I^(B). Пусть также начальное сообщение, представленное в первичном алфавите, содержит п символов, а закодированное сообщение — т символов. Если начальное сообщение содержит I_st(A) инфы, а закодированное — I_fin(B), то условие обратимости кодировки, т.е. неисчезновения инфы при кодировке, разумеется, может быть записано последующим образом:

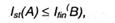
смысл которого в том, что операция обратимого кодировки может прирастить количество инфы в сообщении, но не может его уменьшить. Но любая из величин в данном неравенстве может быть заменена произведением числа символов на среднее информационное содержание знака, т.е.:

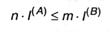
либо

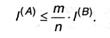
Отношение т/п, разумеется, охарактеризовывает среднее число символов вторичного алфавита, которое приходится использовать для кодировки 1-го знака первичного алфавита — будем именовать его длиной кода либо длиной кодовой цепочки и обозначим К(А,В). Как следует

Обычно N > М и I(А) > I(В), откуда К(А,В) > 1, т.е. один символ первичного алфавита представляется несколькими знаками вторичного. Так как методов построения кодов при фиксированных алфавитах А и В существует огромное количество, появляется неувязка выбора (либо построения) лучшего варианта — будем именовать его хорошим кодом. Выгодность кода при передаче и хранении инфы — это экономический фактор, потому что более действенный код позволяет затратить на передачу сообщения меньше энергии, также времени и, соответственно, меньше занимать линию связи; при хранении употребляется меньше площади поверхности (объема) носителя. При всем этом следует сознавать, что выгодность кода не схожа временной выгодности всей цепочки кодирование-передача-декодирование; вероятна ситуация, когда за внедрение действенного кода при передаче придется рассчитываться тем, что операции кодировки и декодирования будут занимать больше времени и других ресурсов (к примеру, места в памяти технического устройства, если эти операции выполняются с его помощью).

Как надо из (3.1), мало вероятным значением средней длины кода будет:

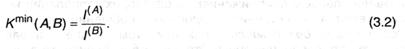
Данное выражение следует принимать как соотношение оценочного нрава, устанавливающее нижний предел длины кода, но, из него непонятно, в какой степени в реальных схемах кодировки может быть приближение К(А,В) к K^min(А,В). По этой причине для теории кодировки и теории связи важное значение имеют две аксиомы, доказанные Шенноном. 1-ая — ее мы на данный момент разглядим — затрагивает ситуацию с кодировкой при отсутствии помех, искажающих сообщение. 2-ая аксиома относится к реальным линиям связи с помехами и будет дискуссироваться.

1-ая аксиома Шеннона, которая именуется основной аксиомой о кодировке при отсутствии помех, формулируется последующим образом: