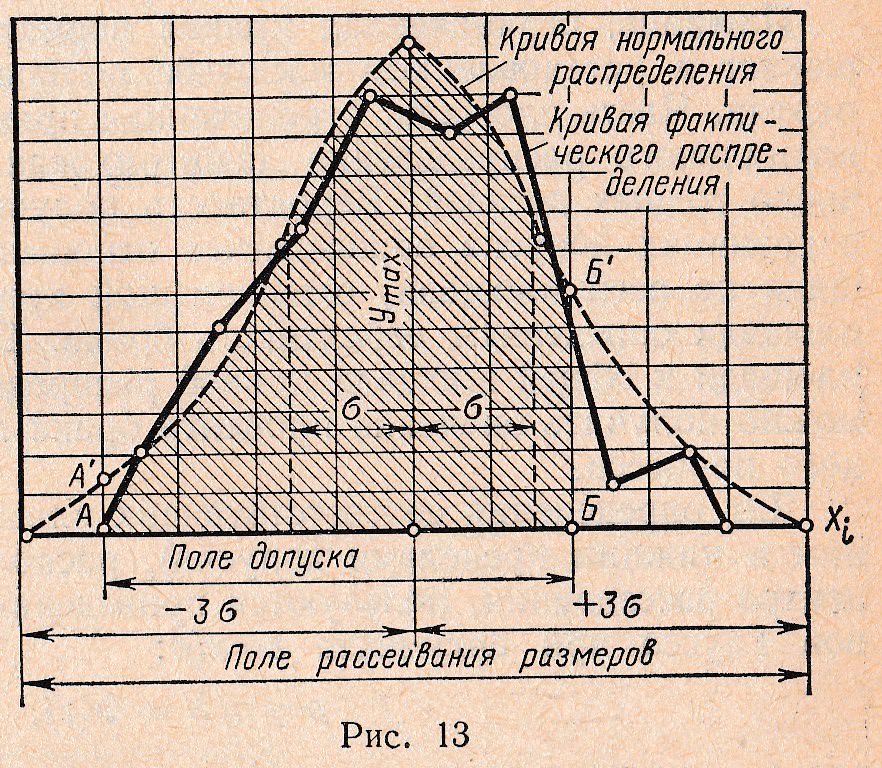
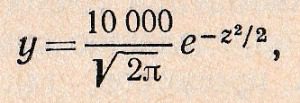Кривые рассеивания фактических размеров, полученные на основании наблюдений, имеют вид ломаных линий (сплошная линия на рис. 13). Поэтому вывод каких-либо закономерностей, имеющих общее значение, на основании рассмотрения этих кривых является затруднительным. Для сопоставления и определения степени приближения кривой рассеивания фактических размеров к теоретической кривой распределения вычерчивают обе кривые в одинаковом масштабе.
Зная средний размер Lcp и среднее квадратичное отклонение о можно построить кривую нормального распределения для каждого наблюдения, при этом среднеарифметическое значение размера определит положение кривой нормального распределения (центр группирования), а среднеквадратичное отклонение размера — высоту и растянутость этой кривой.
Графическое построение кривой нормального распределения может быть упрощено, если воспользоваться значениями ординат у, вычисленных при σ = 1, т. е. для уравнения:
где π = 3,14; е — основание натуральных логарифмов; z=x/σ; x=Li—Lcp — абсцисса, отсчитываемая от центра группирования. В зависимости от аргумента z величина у имеет следующие значения:
Практически для построения ветви кривой нормального распределения достаточно 5…7 точек, причем первое значение абсциссы, определяющее вершину кривой, необходимо принять х=0, а последнее не должно выходить за пределы х=3σ. После этого определяют z =х/σ и по этим данным находят соответствующие значения у.
Для приведения кривой нормального распределения к тому же масштабу (частоте), что и у кривой рассеивания фактических размеров, ординату у умножают на масштабный коэффициент, тогда:
mi = y[( n∆x/(10 000σ)],
где mi, — ордината кривой нормального распределения в том же масштабе, что и у кривой рассеивания фактических размеров; n — общее число деталей в партии; ∆х — интервал по оси абсцисс, принятый при построении кривой рассеивания фактических размеров (выраженный в тех же единицах, что и σ). После этого точки, полученные на графике при построении теоретической кривой нормального распределения, обводятся плавной линией (пунктирная линия на рис. 13).
Площадь, ограниченная кривой нормального распределения, выражает в установленном масштабе полное число деталей в данной партии. Часть площади, ограниченная прямыми АA’ и ББ’ и кривой нормального распределения (заштрихованная площадь), определяет число годных деталей. Вероятность получения деталей с размерами в границах допуска определяется отношением заштрихованной площади ко всей площади, ограниченной кривой, а незаштрихованные площади определяют вероятность брака. Таким образом, отнеся эти площади к общей площади кривой распределения и умножив на 100, можно получить значение процента брака для данного технологического процесса.
Для определения соответствующих площадей (ограниченных верхним и нижним пределами допуска), расположенных по обе стороны центра рассеивания, пользуются приведенным ранее уравнением кривой Гаусса при аргументе z = х/σ:
р = n/N = Ф(z),
где р — частость (вероятность); n — число благоприятных случаев; N — число возможных случаев; Ф(z) — площадь под одной половинной кривой нормального распределения, ограниченной с одной стороны средним значением (ось симметрии кривой) и с другой стороны — отклонением отдельных значений. Значения величины 1/2 Ф(z) (половины предельных площадей под кривой нормального распределения) приводятся в справочниках.
Более высоким этапом повышения точности производства является переход к синтезу, т. е. к определению суммарной погрешности как отдельных технологических процессов, так и всей технологической цепи изготовления деталей, а также машины или механизма в целом. Особое значение синтез приобретает в связи с существенным повышением степени автоматизации производственных процессов, что обусловливает необходимость не только прогнозировать точность каждой составляющей технологического процесса, но и обеспечивать решение задачи автоматического управления процессом в целях получения требуемой точности изделий при минимальных производственных затратах. При этом методика анализа и синтеза погрешностей деталей, а также машин и приборов в целом предусматривает обеспечение точности в комплексе, начиная с расчетно-конструкторских разработок при проектировании технологических процессов всех стадий производства и заканчивая проектированием и созданием средств измерений и контроля.
Базируясь на анализе структурных схем и функциональных связей параметров характеристики изделия, можно разработать математические модели (математическое описание) закономерностей и взаимосвязей, определяющих требования к точности на основе заданного качества на выходе технологического процесса, т. е. создать условия, обеспечивающие стабильность технологии производства.