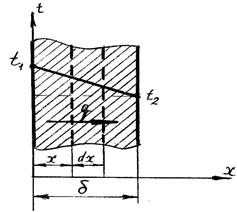
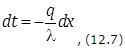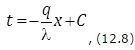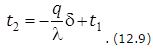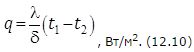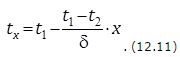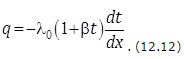Рис. 12.1 Однородная плоская стенка
Рассмотрим плоскую стенку толщиной d, изготовленную из однородного материала (рис. 12.1), коэффициент теплопроводности которого постоянен и равен l. На наружных поверхностях стенки поддерживаются постоянные температуры t1 и t2.
Изменение температуры происходит только в направлении оси Х. В этом случае температурное поле одномерно, изотермические поверхности плоские и располагаются перпендикулярно оси Х. Выделим внутри стенки на расстоянии х от левого края слой толщиной dx (см. рис. 12.1) Этот слой будет ограничиваться двумя плоскостями, изображенными пунктирными линиями, поверхности которых будут изотермичны. Рассматривая стационарный процесс теплопроводности (q = const), на основании закона Фурье можно записать:
Разделим переменные и проинтегрируем полученное выражение:
Постоянную интегрирования C можно определить из граничных условий:
| при X = 0 | t = t1 = C |
| при X = d | t = t2 |
Подставляя эти значения в уравнение (12.8), получим:
Отсюда:
Следовательно, количество тепла, передаваемое через один квадратный метр площади стенки в единицу времени, прямо пропорционально коэффициенту теплопроводности l и разности температур наружных поверхностей и обратно пропорционально толщине стенки d. Уравнение (12.10) является расчётной формулой теплопроводности плоской стенки. Оно связывает между собой четыре величины — удельный тепловой поток q, теплопроводность l, толщину стенки d и разность температур. Зная значения любых трех величин (или задаваясь), можно определить четвертую. Необходимо запомнить, что отношение λ/δ называют тепловой проводимостью стенки, а обратную величину δ/λ — термическим (или тепловым) сопротивлением теплопроводности.
Если в уравнение (12.8) подставить найденные значения 
и C = t1, то можно получить уравнение температурной кривой:
Принимая значение теплопроводности постоянным, получаем изменение температуры по линейному закону. В действительности, из-за того что теплопроводность является функцией температуры, формула температурной кривой будет сложнее. Для строительных и изоляционных материалов λ = λ0(1 + βt) и поэтому:
Разделив переменные, проинтегрировав и найдя из граничных условий константу интегрирования, можно получить уравнение температурной кривой с учетом меняющейся в различных температурных зонах теплопроводности.