Пример 1
Параллельно с лампой мощностью 100 Вт включили электроплитку мощностью 400 Вт. Напряжение в сети 127 В. Какое напряжение на лампе до и после включения электроплитки, если сопротивление подводящих проводов составляет 3 Ом? Указанные мощности тока лампы и плитки соответствуют напряжению 327 В.
Дано: Р1=100 Вт — мощность лампы, Р2=400 Вт —мощность электроплитки, U=127 В — напряжение в сети, R0=3 Ом — сопротивление подводящих проводов.
Найти: U1` — напряжение на лампе до включения электроплитки; U1« — напряжение на лампе и плитке после включения последней.
Решение. Для решения задачи необходимо вычислить токи в цепи до и после включения плитки. Для этого нужно знать общее сопротивление цепи в том и другом случаях. Зная токи и сопротивление потребителей, найдем искомые величины. Из выражения для мощности найдем сопротивления обоих потребителей:
R1=U2/P1, R2=U2/P2
Запишем общее сопротивление цепи при различной нагрузке и токи в обоих случаях: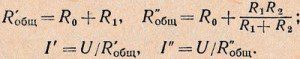
Подставляя числовые значения, находим сопротивления цепи:
Так как потребители и провода в обоих случаях соединены последовательно, напряжение 127В распределится пропорционально сопротивлениям потребителей и проводов: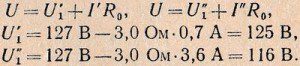
Ответ. В результате параллельного подключения к лампе плитки напряжение на зажимах лампы понизилось от 125 до 116 В.
Пример 2
В сеть с напряжением 220В последовательно включаются две лампы мощностью 60 и 250 Вт, рассчитанные на напряжение 110В каждая. Как распределится напряжение на лампах? Какова мощность, потребляемая каждой лампой? Сколько тепла выделится за 30 мин горения каждой из ламп?
Дано: U=220 В — напряжение в сети, n=2 — количество ламп, Р1=60 Вт — мощность первой лампы, Р2=250 Вт — мощность второй лампы, U1=U2=110 В—напряжение (номинальное) на лампах, t=1800 с — время.
Найти: U1` — напряжение на первой лампе; U2` — напряжение на второй лампе; P1`и P2` — мощности, потребляемые каждой лампой при их последовательном включении в сеть; Q1`и Q2`— количества выделенного ими тепла.
Решение. Напряжения на последовательно соединенных лампах прямо пропорциональны их сопротивлениям. Поэтому сначала вычислим сопротивления ламп:![]()
По закону Ома найдем ток в лампах:![]()
Подставляя числовые данные, находим сопротивления каждой из ламп и напряжения на них: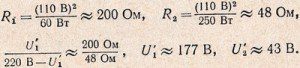
Зная ток, протекающий через лампы, их сопротивление и время, вычислим мощности, потребляемые лампами при их последовательном включении, и количества выделившегося в них тепла:
Ответ. Напряжения на лампах соответственно равны: U1`≈177 В, U2`≈43 В; мощности: P1`≈159Вт, P2`≈39Вт; количества тепла: Q1`≈2,9*105 Дж Q2`≈0,7*105 Дж.
Пример 3
Свинцовый предохранитель, включенный в сеть, состоящую из медного провода сечением 5 мм2, плавится, если провод нагревается на 25 К. Каково сечение свинцовой проволоки предохранителя? Начальная температура свинцового предохранителя 293 К.
Дано: S1=5 мм2=5,0*10-6 м2 — площадь поперечного сечения медного провода, р1=1,68*10-8 Ом*м, р2=2,07*10-7 Ом*м — удельные сопротивления соответственно меди и свинца, c1=3,8*102 Дж/(кг*К), с2= 1,2*102 Дж/(кг*К) — удельные теплоемкости соответственно меди и свинца, D1=8,9*103 кг/м3, D2=1,14*104кг/м3 — плотности соответственно меди и свинца, Т1=293 К — начальная температура свинца, TПЛ=600К — температура плавления свинца, λ=2,5*104 Дж/кг — удельная теплота плавления свинца, ∆T=25 К — приращение температуры медного провода.
Найти: S2— площадь поперечного сечения свинцовой проволочки предохранителя.
Решение. Количество тепла Q1, пошедшее на нагревание медного провода, можно выразить в виде:
Q1=c1S1l1D1∆T
Это количество тепла, полученное в результате прохождения электрического тока, равно
Q1=I2R1t=I2tp1l1/S1
Приравнивая правые части написанных выражений для Q1, получим:
I2tp1l1/S1= c1S1l1D1∆T
На основании тех же рассуждений запишем выражение для Q2 — количества тепла, выделенного током в свинцовом проводнике:
Q2=I2R2t=I2tp2l2/S2
Это количество тепла было потрачено на нагревание свинцового проводника до температуры плавления и на его плавление:
Q2=S2l2D2[c2(TПЛ-T1)+λ]
Приравняв правые части, получим:
I2tp2l2/S2= S2l2D2[c2(TПЛ-T1)+λ]
Учитывая, что ток и время протекания процесса в обоих случаях одинаковы, исключим эти величины путем деления Q1 на Q2: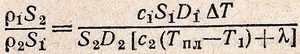
Полученное выражение позволяет определить площадь 52 поперечного сечения свинцовой проволоки:![]()
Подставляя в него числовые данные, находим:![]()
Ответ. Площадь поперечного сечения свинцовой проволоки предохранителя равна 2,5*10-6 м2, или 2,5 мм2.
Спасибо за сборник. Именно он помог успешно сдать экзамен по физике.