Отыскать значение. S3(I22, I11,01). В данном случае конечная функция будет двуместной (п = 3 — 1 = 2), как следует h(х1, х2) = I22(I11, 01) = I22(x1, 0) = 0 .
Примитивная рекурсия
Пусть заданы какие-либо числовые частичные функции: n-местная g(x1,…, хn) и (п + 2)-местная h(x1, …, xn, k, у). Молвят, что (п + 1)-местная частичная функция f появляется из функций д и h средством примитивной рекурсии, если для всех натуральных значений х1;…, xn, у справедливо:
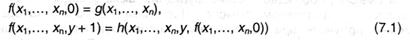
Так как областью определения функций является огромное количество всех натуральных чисел, частичная функция f, удовлетворяющая условиям (7.1), существует для каждых частичных функций g и h и функция эта будет единственной. Условия (7.1) задают также последовательность определения значений f на разных шагах рекурсии:
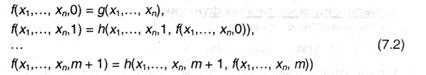
Символически примитивная рекурсия обозначается f = R(g,h); в этой записи R рассматривается как знак двуместной частичной операции, определенной на огромном количестве всех частичных функций. Из соотношений (7.2) вытекает, а именно, что если g и h являются везде определенными, то и f также является везде определенной. Из (7.2) видно также то принципиальное событие, что если умеем отыскивать значения функций g и h, то значения функции f(a1,…, an, т + 1) можно вычислять «механически», находя поочередно значения на прошлых шагах. Введем определение.
Частичная функция f(x1,…, xn) именуется примитивно рекурсивной, если ее можно получить конечным числом операций суперпозиции и примитивной рекурсии, исходя только из простых функций S1, 0n и Imn.
Если операции суперпозиции и примитивной рекурсии применить к везде определенным функциям, в итоге будет получена также везде определенная функция. А именно, все примитивно рекурсивные функции везде определены.