Как надо из приведенного выше определения, структурирование данных подразумевает существование (либо установление) меж ними каких-либо отношений (связей). Зависимо от нрава этих отношений можно выделить несколько классификационных признаков структур данных.

Первым из их разглядим отношение порядка. По порядку данных структуры делятся на упорядоченные и неупорядоченные.

В упорядоченных структурах элементы располагаются по порядку в согласовании со значением некого признака. Более обычным признаком является порядковый номер элемента:, установление порядка в согласовании с номером именуется нумерацией. При всем этом если весь набор имеет один общий идентификатор (к примеру, М), то отдельным данным присваиваются собственные идентификаторы — индексы (к примеру, М₅ либо М_b). В большинстве случаев индекс задается целым числом, хотя это необязательно -в качестве индекса может выступать хоть какой символ из конечного алфавита. Словарный порядок индексов определяет отношение следования меж элементами структуры, т.е. элемент М₆ следует за элементом М₅, а элемент М_а размещается перед элементом М_b. Примером структур, в каких упорядочение делается по номеру элемента, являются массивы. Порядковый номер элемента можно считать наружным признаком, который может присваиваться элементу независимо от его значения. К примеру, регистрационный номер документа определяется только временем его поступления в учреждение, а не его содержанием. Кроме нумерации в структурах данных употребляется упорядочение по значению некого внутреннего признака, к примеру, размещение фамилий в алфавитном порядке либо группы компаний в порядке убывания их рентабельности -такое упорядочение именуется ранжированием.

Примером неупорядоченных структур являются, огромного количества — в их не определен порядок частей; единственное, что можно установить для каких-либо определенных данных, так это их принадлежность (либо не принадлежность) избранному огромному количеству.

Последующим классификационным признаком структур является однородность. К однородным относятся структуры, содержащие простые данные только 1-го типа. Неоднородные структуры объединяют данные различных типов. Примерами однородных структур являются массивы, огромного количества, стеки. К неоднородным структурам относятся записи.

Еще одним признаком является нрав отношений меж элементами. По обоюдной подчиненности частей структуры данных разделяются на линейные и нелинейные.

В линейных структурах все элементы равноправны. К ним относятся массив, огромное количество, стек, очередь.

В нелинейных структурах меж элементами есть дела подчиненности либо они могут быть связаны логическими критериями. К ним относятся деревья, графы, фреймы.

Основываясь на выделенных классификационных признаках, разглядим и охарактеризуем некие структуры данных.

Массив

Массив — упорядоченная линейная совокупность однородных данных.

Комментарии к определению:

• термин «упорядоченная» значит, что элементы массива пронумерованы;
• термин «линейная» свидетельствует о равноправии всех частей;
• термин «однородных» значит последующее: в этом случае, когда массив формируется из простых данных, это могут быть данные только 1-го какого-то типа, к примеру, массив чисел либо массив знаков; но, вероятна ситуация, когда элементами массива окажутся сложные (структурные) данные, к примеру, массив массивов — в данном случае «однородных» значит, что все элементы имеют схожую структуру и размер.

Количество индексов, определяющих положение элемента в массиве, именуется мерностью массива.

Так, если индекс единственный, массив именуется одномерным; нередко таковой массив именуют также вектором, строчкой либо столбцом. Для записи частей одномерного массива употребляется обозначение m_i; в языках программирования приняты обозначения m(i) либо m[i].

Массив, элементы которого имеют два индекса, именуется двумерным либо матрицей. Пример обозначения: G [3,5]; при всем этом 1-ый индекс является номером строчки, а 2-ой индекс — номером столбца, на скрещении которых находится данный элемент.

Массивы с 3-мя индексами именуются трехмерными и т.д. Наибольшая мерность массива может быть ограничена синтаксисом неких языков программирования, или не иметь таких ограничений.

Наибольшее значение индексов определяет размер массива. Размер массива указывается в блоке описания программки, так как при выполнении программки для хранения частей массива резервируется нужный объем памяти. Если в процессе выполнения программки размер массива не меняется (либо не может быть изменен), то в данном случае молвят о массивах фиксированного размера; если определение размеров массива либо их изменение происходит по ходу работы программки, то такие массивы именуются динамическими (динамически описываемыми).

Допустимый набор операций над элементами массива определяется типом данных (простых либо структурированных), из которых массив сформирован. В неких языках программирования над массивом в целом определена операция присваивания М := <выражение> — в данном случае всем элементам массива присваивается однообразное значение, равное вычисленному значению выражения; вероятна также операция присваивания для 2-ух схожих по типу, размеру и размерности массивов М2:= М1 — делается поэлементное присваивание значений (M2(i,j,k…) := M1(i,j,k…)).

Особенное место занимают символьные массивы — они именуются строчками либо строковыми данными (к примеру, тип String в PASCAL’e). С ними вероятен целый набор операций, неопределенных для одиночных символьных данных. Сначала, это операция конкатенации (объединения) строк с сформированием новейшей строчки. Кроме этого имеются операции замещения части строчки, также определения ее числовых черт.

Стек, очередь

Стек (магазин) и очередь являются упорядоченными, линейными, неоднородными структурами. Эти структуры реализуются в виде особым образом организованных областей ОЗУ компьютера или в качестве самостоятельных блоков памяти. В стеке ячейки памяти (либо регистры стековой памяти) соединяются вместе таким образом, что при занесении данных в первую ячейку содержимое всех других двигается в примыкающие вниз, при считывании — содержимое двигается ввысь по ячейкам, как показано на рис. 6.2. Другими словами, вход в стек вероятен только через первую ячейку (верхушку стека), потому извлекаться первой будет та информация, которая была занесена последней*, подобно пассажиру переполненного автобуса.

* Нередко стек именуют памятью типа LIFO (Last-In First-Out: «последним вошел — первым вышел»).

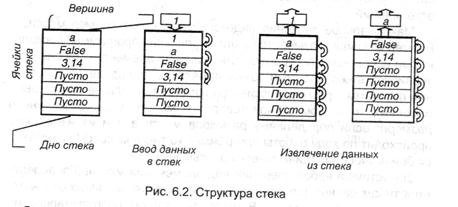
Отличие очереди от стека исключительно в том, что извлечение инфы делается в порядке «первым вошел — первым вышел», т.е. со дна стека.

Таким образом, данные имеют порядок расположения и они равноправны — потому структура является упорядоченной и линейной. Но в общем случае в ячейках стека могут содержаться данные различных типов — по этому признаку структура оказывается неоднородной.

Описанный метод организации данных оказывается комфортным при работе с подпрограммами, обслуживании прерываний, решении многих задач.

Дерево

Дерево либо иерархия является примером нелинейной структуры. В ней элемент каждого уровня (кроме самого верхнего) заходит в один и только один элемент последующего (более высочайшего) уровня. Элемент самого высочайшего уровня именуется корнем, а самого нижнего уровня — листьями.

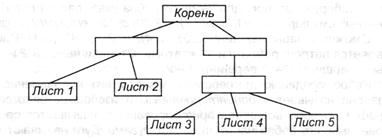
Схема таковой структуры показана на рисунке. Отдельные элементы могут быть однородными либо нет. Примером схожей организации служат файловые структуры на наружных запоминающих устройствах компьютера.

Граф

Нередко дела меж данными представляются в виде графа — совокупность точек и линий, в какой любая линия соединяет две точки. В информатике точка получает смысл элемента структуры (системы, данных и пр.), а полосы — смысл дела меж элементами. Познакомимся с рядом определений, связанных с внедрением графов.

Точки именуются верхушками графа, полосы — ребрами. Если ребро соединяет две верхушки, то молвят, что ребро инцидентно этим верхушкам, а сами верхушки именуются смежными. Число ребер, инцидентных верхушке, именуется степенью верхушки. Если два ребра инцидентны одной и той же паре вершин, они именуются кратными. Ребро, у которого совпадают обе верхушки, именуется петлей.

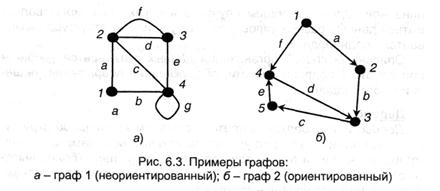
На рис. 6.3,а. граф 1 задается перечнем вершин {1,2,3,4} и перечнем ребер, в каком для каждого ребра указывается пара инцидентных ему вершин: а(1,2); b(1,4); с(2,.4); 6(2,3); е(3,4); f(2,3); g(4,4).

Смежные пары вершин: (2,3), (2,4), (1,2), (1,4), (3,4). Ребро д является петлей; ребра d и f — кратные. Степени вершин 2 и 4 равны 4; верхушки 3-3; верхушки 1 — 2.

Ребро, соединяющие верхушки, может иметь направление — тогда оно именуется нацеленным и изображается стрелкой. Граф, в каком все ребра направленные, именуется нацеленным; его ребра нередко именуют дугами. Дуги именуют кратными, если они соединяют одни и те же верхушки и совпадают по направлению. При обозначении дуги всегда поначалу указывается верхушка, из которой она начинается, к примеру, на рис. 6.3,б (2,3).

Маршрут — это последовательность ребер, в каком конец предшествующего ребра совпадает с началом последующего, к примеру, а, с, е на графе 1. Маршрут, в каком конечная верхушка совпадает с исходной, именуется циклом, к примеру, с, е, d на графе 2. Граф именуется связным, если меж хоть какими 2-мя его верхушками имеется маршрут. Связный граф с п верхушками содержит более п-1 ребер.

По рассмотренной ранее систематизации граф является упорядоченной, нелинейной, неоднородной структурой. Понятие графа благодаря его наглядности и высочайшей общности в информатике выступает в качестве основного средства описания структур данных, систем, порядка выполнения действий. Примером может служить блок-схема программки.

Исходя из убеждений практического использования большой энтузиазм представляет очередной тип данных, образующих упорядоченную, линейную, неоднородными структуру. Такую структуру можно рассматривать как массив неоднородных структурированных данных.

Структура именуется таблицей, а ее отдельная строчка — записью (логической записью). Ввиду большой значимости данной структуры она будет рассмотрена более тщательно.