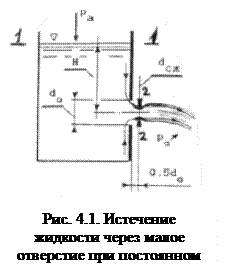
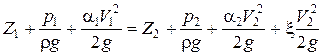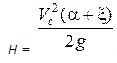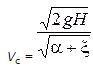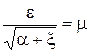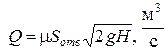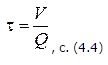Рассмотрим случай истечения жидкости при постоянном напоре (рис. 4.1). Для получения расчетной зависимости запишем уравнение Бернулли для двух сечений 1 – 1 и 2 – 2 относительно плоскости сравнения О-О проведенной по дну судна.
Примем к сведению, что жидкость вытекает в воздушное пространство с атмосферным давлением, а на поверхности жидкости также давление атмосферное, и имеет место только местное сопротивление. Тогда:
где ξ – коэффициент местного сопротивления отверстия.
Для первого сечения Z1 = H, V1 = 0, для второго сечения Z2 = 0, V2 = Vc. Тогда уравнение Бернулли приобретает вид:
где Vc – скорость жидкости в сжатом сечении; 
α – коэффициент неравномерности распределения скоростей по сечению.
Решив уравнение относительно Vc, получим:
Расход жидкости тогда составит:
Q = Vc Sc,
где Sc – площадь сжатого сечения.
Имея в виду, что пользоваться величиной площади сжатого сечения неудобно, перейдем к площади отверстия, используя коэффициент сжатия струи:
Sc = Sотв ε.
Тогда расход жидкости через отверстие:
Формула расхода примет вид:
где μ – коэффициент расхода малого отверстия, изменяющийся в пределах: ![]() ;
;
Н – напор, под действием которого происходит истечение жидкости.
Иногда требуется рассчитать время истечения заданного объема жидкости. Если напор (Н) при этом не изменяется, то время можно рассчитать как разность от деления объема на секундную производительность отверстия:
При изменении напора от Н до нуля, то есть при опорожнении (или заполнении резервуара) средний напор будет равен H/2, и время истечения соответственно увеличивается.