Рассматривая формы представления информации, отметили то событие, что, естественной для органов эмоций человека является аналоговая форма, универсальной все таки следует считать дискретную форму представления информации при помощи некого набора символов. А именно, конкретно таким образом представленная информация обрабатывается компом, передается по компьютерным и неким другим линиям связи. Сообщение есть последовательность символов алфавита. При их передаче появляется неувязка определения знака: каким образом прочесть сообщение, т.е. по приобретенным сигналам установить начальную последовательность символов первичного алфавита. В устной речи это достигается внедрением разных фонем (главных звуков различного звучания), по которым и отличаются знаки речи. В письменности это достигается разным начертанием букв и предстоящим нашим анализом написанного. Как данная задачка может решаться техническим устройством, разглядим позже. На данный момент для принципиально, что можно воплотить некую функцию (механизм), средством которой выделить из сообщения тот либо другой символ. Но возникновение определенного знака (буковки) в определенном месте сообщения — событие случайное. Как следует, узнавание (отождествление) знака просит получения некой порции информации. Можно связать эту информацию с самим знаком и считать, что символ несет внутри себя (содержит) некое количество информации. Попробуем оценить это количество.
Начнем с самого грубого приближения (будем именовать его нулевым, что отражается индексом у получаемых величин) — представим, что возникновение всех символов (букв) алфавита в сообщении равновероятно. Тогда для британского алфавита пe = 27 (с учетом пробела как самостоятельного знака); для российского алфавита nr = 34. Из формулы Хартли (2.15) находим:
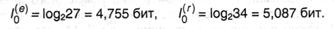
Выходит, что в нулевом приближении со знаком российского алфавита в среднем связано больше информации, чем со знаком британского. К примеру, в российской буковке «а» информации больше, чем в «а» британской! Это, непременно, не значит, что британский язык — язык Шекспира и Диккенса — беднее, чем язык Пушкина и Достоевского. Лингвистическое достояние языка определяется количеством слов и их сочетаний, и никак не связано с числом букв в алфавите. Исходя из убеждений техники это значит, что сообщения из равного количества знаков будет иметь разную длину (и соответственно, время передачи) и большими они окажутся у сообщений на российском языке.
В качестве последующего (первого) приближения, уточняющего начальное, попробуем учитывать то событие, что относительная частота, т.е. возможность возникновения разных букв в тексте (либо сообщении) различна. Разглядим таблицу средних частот букв для российского алфавита, в который включен также символ «пробел» для разделения слов с учетом неразличимости букв «е» и «ё», также «ь» и «ъ» (так принято в телеграфном кодировке), получим алфавит из 32 символов со последующими вероятностями их возникновения в российских текстах:
Таблица 2.1

Для оценки информации, связанной с выбором 1-го знака алфавита с учетом неравной вероятности их возникновения в сообщении (текстах) можно пользоваться формулой (2.14). Из нее, а именно, следует, что если рi — возможность (относительная частота) знака номер i данного алфавита из N символов, то среднее количество информации, приходящейся на один символ, равно:

Это и есть именитая формула К. Шеннона*, с работы которого «Математическая теория связи» (1948) принято начинать отсчет возраста информатики, как самостоятельной науки [46]. Объективности ради следует увидеть, что и в нашей стране фактически сразу с Шенноном велись подобные исследования, к примеру, в том же 1948 г. вышла работа А. Н. Колмогорова «Математическая теория передачи информации».
* По сути формула Шеннона, как и формула Хартли, вначале была записана для энтропии. Но для нашего изложения более комфортной представляется форма записи через понятие информации.
В общем случае информация, которая содержится в сообщении, может зависеть от того, в какой момент времени оно добивается приемника. К примеру, несвоевременное сообщение о погоде, разумеется, не несет той же информации, что и своевременное. Предельным случаем оказывается ситуация, когда вся переносимая сообщением информация определяется временем его поступления; к примеру, бой часов либо звонок с урока. Но может быть существование сообщений, в каких содержащаяся в их информация не находится в зависимости от времени поступления. А именно, такая ситуация реализуется в этом случае, если возможность повстречать в сообщении какой-нибудь символ i не находится в зависимости от времени, поточнее, она схожа во все моменты времени и равна относительной частоте этого знака рi во всей последовательности символов. Потому вероятности символов (относительные частоты) определяются для сообщений (текстов), содержащих огромное число знаков с тем, чтоб проявились статистические закономерности, и дальше числятся постоянными во всех сообщениях данного источника.
Сообщения, в каких возможность возникновения каждого отдельного знака не изменяется с течением времени, именуются шенноновскими, а порождающий их отправитель — шенноновским источником.
Если сообщение является шенноновским, то набор символов (алфавит) и связанная с каждым знаком информация известны заблаговременно. В данном случае интерпретация сообщения, представляющего из себя последовательность сигналов, сводится к задачке определения знака, т.е. выявлению, какой конкретно символ находится в данном месте сообщения. А такая задачка, как уже удостоверились в прошлом параграфе, может быть решена серией парных выборов. При всем этом количество информации, находящееся в знаке, служит мерой издержек по его выявлению.
Теория информации строится конкретно для шенноновских сообщений, потому в предстоящем будем считать это начальным положением (условием использования) теории и рассматривать только такие сообщения.
Применение формулы (2.17) к алфавиту российского языка дает значение средней инфы на символ I1(r) = 4,36 бит, а для британского языка I1(e) = 4,04 бит, для французского I1(f) = 3,96 бит, для германского I1(d) — 4,10 бит, для испанского I1(s) = 3,98 бит. Как лицезреем, и для российского, и для британского языков учет вероятностей возникновения букв в сообщениях приводит к уменьшению среднего информационного содержания буковкы, что, кстати, подтверждает справедливость формулы (2.7).
Несовпадение значений средней инфы для британского, французского и германского языков, основанных на одном алфавите, связано с тем, что частоты возникновения схожих букв в их различны.
Последующими приближениями при оценке значения инфы, приходящейся на символ алфавита, должен быть учет корреляций, т.е. связей меж знаками в словах. Дело в том, что в словах буковкы возникают не в всех сочетаниях; это понижает неопределенность угадывания последующей буковки после нескольких, к примеру, в российском языке нет слов, в каких встречается сочетание щц либо фъ. И напротив, после неких сочетаний можно с большей определенностью, чем незапятнанный случай, судить о возникновении последующей буковки, к примеру, после всераспространенного сочетания пр- всегда следует гласная буковка, а их в российском языке 10 и, как следует, возможность угадывания последующей буковки 1/10, а не 1/33. Как указывается в книжке Л. Бриллюэна [7, с.46], учет в британских словах двухбуквенных сочетаний понижает среднюю информацию на символ до значения I2(e) = 3,32 бит, учет трехбуквенных — до I3(e) = 3,10 бит. Шеннон смог примерно оценить I5(e) ≈ 2,1 бит и I8(e) = 1,9 бит. Подобные исследования для российского языка дают: I2(r) = 3,52 бит; I3(r) = 3,01 бит. Последовательность I0, I1, I2… является убывающей в любом языке. Экстраполируя ее на учет нескончаемого числа корреляций, можно оценить предельную информацию на символ в данном языке I¥, которая будет отражать наименьшую неопределенность, связанную с выбором знака алфавита без учета семантических особенностей языка, в то время как I0 является другим предельным случаем, так как охарактеризовывает самую большую информацию, которая может содержаться в знаке данного алфавита. Шеннон ввел величину, которую именовал относительной избыточностью языка:

Избыточность является мерой никчемно совершаемых других выборов при чтении текста. Данная величина указывает, какую долю излишней информации содержат тексты данного языка; излишней в том отношении, что она определяется структурой самого языка и, как следует, может быть восстановлена без очевидного указания в буквенном виде.
Исследования Шеннона для британского языка дали значение I¥ ≈ 1,4÷1,5 бит, что по отношению к I0 = 4,755 бит делает избыточность около 0,68. Подобные оценки демонстрируют, что и для других европейских языков, в том числе российского, избыточность составляет 60 — 70%. Это значит, что в принципе может быть практически трехкратное (!) сокращение текстов без вреда для их содержательной стороны и выразительности. К примеру, телеграфные тексты делаются короче за счет отбрасывания союзов и предлогов без вреда для смысла; в их же употребляются совершенно точно интерпретируемые сокращения «ЗПТ» и «ТЧК» заместо полных слов (эти сокращения приходится использовать, так как знаки «.» и «,» не входят в телеграфный алфавит). Но такое «экономичное» представление слов понижает разборчивость языка, уменьшает возможность осознания речи при наличии шума (а это одна из заморочек передачи информации по реальным линиям связи), также исключает возможность локализации и исправления ошибки (написания либо передачи) при ее появлении. Конкретно избыточность языка позволяет просто вернуть текст, даже если он содержит огромное число ошибок либо неполон (к примеру, при отгадывании кроссвордов либо при игре в «Поле чудес»). В этом смысле избыточность есть определенная страховка и гарантия разборчивости.