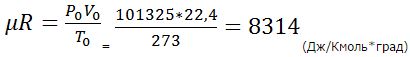Идеальный газ точно подчиняется уравнению Клапейрона, и поэтому оно называется уравнением состояния идеального газа. Для одного кг газа уравнение Клапейрона имеет вид:

pv = RT (6.20)

Если проанализировать физический смысл газовой постоянной:

R = pv/T (6.21)

где pv – это удельная механическая работа, полученная в результате расширения 1 кг газа,

то R – это удельная работа расширения 1 кг газа при нагревании его на один градус, (Дж/кг·К).

[Киломоль (Кмоль, килограмм – молекула)- это количество килограммов вещества, численно равное его молекулярной массе].

Для этого умножим обе части уравнения (6.20) на массу одного Киломоля µ (кг/Кмоль)

pvµ = µRT (6.22)

Произведение vµ представляет собой объём одного Киломоля газа:

vµ = V; (м³/Кмоль) (6.23)

Идеальные газы подчиняются закону Авогадро. При одинаковых температурах и давлениях объёмы, занимаемые одним Киломолем любого идеального газа одинаковы. При нормальных условиях (при P₀ = 101325 Па и T₀ = 273 К) один Киломоль идеального газа занимает объём V_µ = 22,4 м³/Кмоль и если подставить эти значения в уравнение (6.22), то окажется что произведение µR является величиной постоянной:

Так как эта величина µR одинакова для всех идеальных газов, она называется универсальной газовой постоянной и обозначается R_µ

µR = R_µ = 8314 (Дж/Кмоль*град) (6.24)

Уравнение (6.22) можно представить в виде:

pVµ = 8314 Т (6.25)

Уравнение (6.24) называется уравнением Менделеева – Клапейрона.

Зная константу R_µ = 8314 можно определить величину газовой постоянной для одного килограмма любого газа:

R = 8314/µ (Дж/кг*град) (6.26)

Из закона Авогадро вытекает, что плотность газов при одинаковых значениях давления P и температуры T прямо пропорциональна их молярным массам:

p₁/p₂ = µ₁/µ₂ (6.27)

Отношение плотностей можно заменить обратным отношением удельных объёмов:

v₂/v₁ = µ₁/µ₂ (6.28)

откуда

v₁µ₁ = v₂µ₂ (6.28)