В справедливости (2.5) можно убедиться конкретно: Пусть опыт α имеет п исходов А₁, А₂, … А_п, которые реализуются с вероятностями р(А₁), р(А₂), … р(А_п), а событие β — т исходов B₁, В₂, … В_т с вероятностями р(В₁), р(В₂), … р(В_т). Непростой опыт α ^ β имеет п∙т исходов типа A_iB_j (i = 1… n, j = 1… т). Как следует:

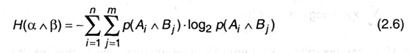
Так как α и β — независимы, то независящими окажутся действия в хоть какой паре A_i ^ B_j. Тогда, согласно (А.9),

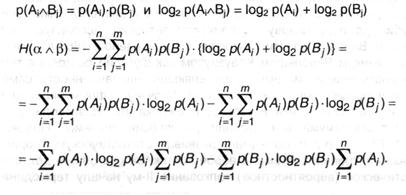
В слагаемых произведено изменение порядка суммирования в согласовании со значениями индексов. Дальше, по условию нормировки (А.7):

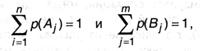
а из (2.4)

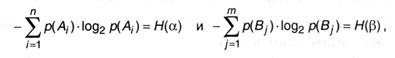
совсем имеем:

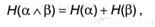
что и требовалось обосновать.

Сейчас разглядим ситуацию, когда имеются два опыта с схожим числом исходов п, но в одном случае они равновероятны, а в другом — нет. Каково соотношение энтропии опытов? Примем без подтверждения* последующее утверждение:

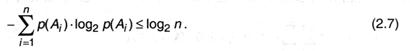
* По мере надобности подтверждение можно отыскать, к примеру, в книжках: А.М. и И.М. Яглом [49, с.73-75]; Л. Бриллюэн [7, с.34-36].