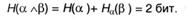Имеется три тела с схожими наружными размерами, но с различными массами х1, х2 и х3. Нужно найти энтропию, связанную с нахождением более томного из их, если ассоциировать веса тел можно только попарно.
Последовательность действий довольно явна: сравниваем вес 2-ух всех тел, определяем из их более тяжелое, потом с ним сравниваем вес третьего тела и избираем больший из их. Так как снаружи тела неразличимы, выбор номеров тел при взвешивании будет случаен, но общий итог от этого выбора не зависит. Пусть опыт ее состоит в сопоставлении веса 2-ух тел, к примеру, 1-го и 2-го. Этот опыт, разумеется, может иметь два финала: А1 – х1 > х2; его возможность р(А1) = 1/2; финал А2 — x1 < х2; также его возможность р(А2) = 1/2.
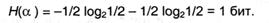
Опыт β — сопоставление весов тела, избранного в опыте α, и 3-го — имеет четыре финала: B1, — х1 > х3, B2 – х1 < х3, B3 — х2 > х3, В4 — х2 < х3; вероятности исходов зависят от реализовавшегося финала α — для удобства представим их в виде таблицы:

Вновь, воспользовавшись формулами (2.8) и (2.9) и с учетом характеристики (1) п.2.1.2, находим:
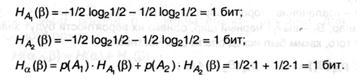
Как следует, энтропия сложного опыта, т.е. всей процедуры испытаний: