Электрическая емкость характеризует способность проводника сохранять электрический заряд в электростатическом поле. Рассмотрим более подробно понятие электрической емкости.

При электризации диэлектрика заряжается только та часть его поверхности, которая подвергалась натиранию или сопри­касалась с другим заряженным телом. Электрический заряд, возбужденный на части поверхности диэлектрика, не может распространиться по всей его поверхности, так как в диэлек­триках все электрические заряды прочно связаны с молеку­лами вещества, лишенными свободы передвижения. Можно, например, зарядить один конец эбонитовой палочки отрица­тельным электричеством, а другой конец — положительным электричеством, и оба этих противоположных по знаку заряда не смогут соединиться друг с другом (Рис. 1).

Рисунок 1. Распределение зарядов в диэлектрике.

Электрические заряды на проводниках ведут себя совер­шенно иначе. Если мы поместим на проводник некоторое ко­личество электронов, они немедленно, отталкиваясь друг от друга, распространятся по всей поверхности проводника, при­чем именно по поверхности, а не по толще проводника.

Если зарядить электричеством проводник удлиненной фор­мы, например металлическую палочку, то наибольшее количе­ство зарядов сосредоточится на ее концах (рис. 2.).

Рисунок 2. Распределение зарядов в проводнике.

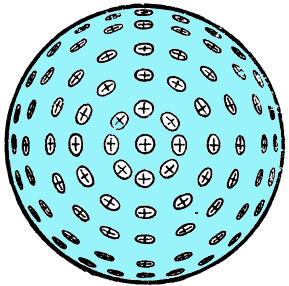
При за­ряде металлического шара электрические заряды распределятся по его поверхности равномерно (рис. 3.). Если этот шар будет пустотелым, то это нисколько не повлияет на распреде­ление зарядов; они также равномерно «расселятся» по наруж­ной поверхности шара, так как каждый из них будет стре­миться уйти подальше от своих одноименных соседей — заря­дов. Это в равной степени относится как к отрицательным зарядам, так и к положительным.

Рисунок 3. Распределение зарядов на поверхности металлического шара.

Свободные электрические заряды, помещенные в каком-либо месте на проводнике, расходятся по его поверхности по­добно воде, растекающейся, например, по дну какого-либо со­суда. Подобно тому, как вода будет растекаться по дну сосуда до тех пор, пока уровень ее не сделается всюду одинако­вым, так и электрические заряды будут «растекаться» по поверхности проводника до тех пор, пока электрический по­тенциал всех точек поверхности не станет одинаковым. Прак­тически этот процесс происходит мгновенно.

Легко сообразить, что потенциал положительно заряжен­ного проводника будет тем выше, чем больше заряд, сообщен­ный проводнику. Это видно хотя бы из такого рассуждения. Представим себе, что мы заряжаем положительным электри­чеством какой-либо уединенный металлический предмет (про­водник), перенося на его поверхность один за другим отдель­ные электрические заряды. По мере накопления на нем элек­тричества на перенесение новых зарядов придется затрачивать все больше и больше работы, так как при переносе каждого следующего заряда нам придется преодолевать силы отталки­вания, действующие со стороны всех предыдущих зарядов, помещенных ранее на проводник. А так как потенциал про­водника характеризуется работой, затраченной на перенесение единичного положительного заряда из бесконечно удаленной точки в какую-либо точку проводника, то с увеличением поло­жительного заряда проводника потенциал его будет повышать­ся (ясно, что потенциал проводника, заряженного отрицатель­ным зарядом, будет отрицателен и с увеличением заряда бу­дет понижаться).

Количественная связь между величиной заряда проводника и его потенциалом очень проста: потенциал проводника прямо пропорционален величине его заряда, т. е. при увеличении за­ряда проводника, например, вдвое потенциал его повышается также вдвое.

Однако, соотношение между зарядом и потенциалом раз­лично для разных проводников. Например, один проводник достаточно зарядить количеством электричества в одну милли­ардную долю кулона, чтобы довести его потенциал до одного вольта, а другому проводнику для этого потребуется заряд, например, в одну стомиллионную долю кулона. Следователь­но, для разных проводников нужны разные количества элек­тричества, чтобы довести их заряд до одного и того же «элек­трического уровня». Поэтому принято считать, что различные проводники обладают различной электрической емкостью.

Электрическая емкость проводника зависит, прежде всего, от его разме­ров, — чем больше размеры проводника, тем больше его ем­кость. Емкость проводника зависит и от других причин, о ко­торых мы еще будем говорить. За единицу электрической ем­кости принимают емкость такого проводника, которому надо сообщить заряд, равный единице количества электричества — одному кулону, чтобы потенциал его повысился также на одну единицу, т. е. на 1 вольт.

Поскольку мы сравнивали электрический потенциал с уров­нем жидкости в сосуде, можно попытаться и далее искать аналогию между емкостью проводника и свойствами сосуда.

Однако, электрическую емкость нельзя отождествлять с ем­костью (вместимостью) сосуда. Действительно, емкость сосу­да указывает, какое наибольшее количество жидкости он мо­жет вместить, между тем как электрическая емкость провод­ника ничего не говорит о том, какое количество электриче­ства может «вместить» проводник. Всякий проводник принци­пиально может вместить любое количество электричества, только с увеличением количества электричества будет повы­шаться потенциал (электрический уровень) проводника и по­вышаться тем быстрее, чем меньше емкость проводника.

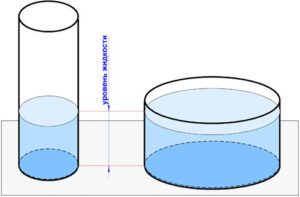
Поэтому электрическую емкость проводника можно было бы сравнить с площадью дна сосуда (мы считаем, что сосуд имеет вертикальные стенки) Действительно, чем больше пло­щадь дна сосуда, тем больше нужно налить в него жидкости для того, чтобы она достигла определенного уровня (рис. 4.).

Рисунок 4. Отличие электрической емкости от обычного понятия емкости.

Итак, электрическая емкость уединенного проводника определяется как отношение количества электричества, сообщенного проводнику, к потенциалу, который при этом приобретает проводник, т. е.

C=Q/U

Если Q выражено в кулонах, а U в вольтах, то единица электрической емкости С получится в фарадах (обозначение Ф.).

Фарада представляет собой слишком крупную величину, никогда не встречающуюся на практике. Поэтому для измере­ния емкости приняты более мелкие единицы — микрофарада (мкФ), нанофарады (нФ) и пикофарады (пФ).

Микрофарада составляет одну миллионную долю фарады, нанофарада одну тысячную микрофарады, а пикофарада — одну миллионную долю микрофарады (или одну тысячную долю нанофарады).

То есть:

1 мкф = 10^-6 Ф;

1 нф = 10^-9 Ф;

1 пф =10^-12 Ф.