Введенное в прошлом параграфе понятие автомата является довольно общим. Накладывая ограничения на составляющие X, Y, Q, Ψ, Θ можно получить личные случаи автоматов. Одним из их являются автоматы без памяти, т.е. устройства, в каких не происходит фиксации внутреннего состояния. Разумеется, в данном случае из общего описания должны быть исключены составляющие Q и Ψ; автомат без памяти задается тройкой компонент < X, Y, Θ>. Соотношение (9.2) воспринимает вид
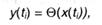
т.е. выходной знак на данном такте определяется только входным эмблемой и не находится в зависимости от ранее поступивших знаков. Как следует, каждый автомат без памяти реализует единственный преобразователь (оператор), который производит «побуквенный перевод» входных последовательностей знаков в выходные.
Пусть имеется дискретное устройство, имеющее п входов х1…..хп и т выходов y1 …, ут. Если данное устройство не обладает памятью, то преобразование входных сигналов в выходные описывается системой уравнений:
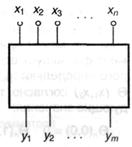
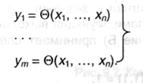
Если входной и выходной алфавиты являются двоичными, то представленная система оказывается системой логических функций, для решения которой можно привлечь аппарат математической логики. Конкретно такие устройства будем рассматривать в предстоящем.
Подобные устройства могут быть построены методом соединения некого набора простых компонент (частей). Эти элементы образуют конечный набор, именуемый базисом, а входящие в него элементы — базовыми. Базис имеет смысл совокупность простых (простых) действий, о которых шла речь в теории алгоритмов, а базовый элемент можно рассматривать в качестве устройства, выполняющее простое действие. Если идет речь о двоичных дискретных устройствах, то базисы строятся из частей, которые реализуют простые логические функции. Напомним, что к таким функциям относятся конъюнкция (логическое И — ^), дизъюнкция (логическое Либо — v), импликация (→), сумма по модулю 2 (Å), эквивалентности (~) и отрицания (логическое НЕ — Ø,). Но меж простейшими функциями имеются соотношения эквивалентности (см. приложение), дозволяющие выразить одни функции через другие. В итоге оказывается, что нет необходимости включать в базис все элементы, реализующие простые логические функции — довольно избрать некое малое их подмножество. Этому условию удовлетворяет базис, построенных на элементах И, Либо и НЕ — он именуется простым, а входящие в него элементы — логическими элементами либо (логическими вентилями). Схемы частей приведены на рис. 9.1. Разглядим каждый их их по отдельности.
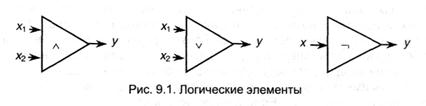
Элемент И (^) имеет два входа, на которые независимо могут подаваться сигналы x1 и х2; любой из сигналов является двоичным, т.е. может принимать одно из 2-ух значений — 1 либо 0; элемент сформировывает единственный выходной сигнал у, значения которого определяются только входными сигналами. Функция выходов Q (x1,x2) согласно табл. Б.1 (см. приложение Б) воспринимает последующие значения:
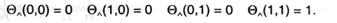
Функция выходов элемента Либо (V) воспринимает последующие значения:
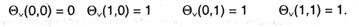
Логический элемент НЕ (Ø) обеспечивает одноместное преобразование (с одним входным сигналом) в согласовании с правилами:
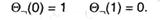
Сочетая базовые элементы по определенным правилам, можно выстроить их сложные объединения — схемы (над данным базисом), способные совершать преобразования, надлежащие, вообщем говоря, хоть каким логическим функциям. Таким образом, схема есть композиция базовых частей, в какой выходы одних частей присоединяются к входам других. Если в таких объединениях частей отсутствуют замкнутые контуры (подача сигнала с выхода элемента на один из его же входов), то появляется класс схем, которые именуются комбинационными. Молвят, что базис обладает свойством полноты, если схемами над ним может быть реализована неважно какая логическая функция (и, как следует, неважно какая система логических функций). А именно, таким свойством обладает простой базис.
Со схемами связано решение 2-ух классов задач — анализа и синтеза. В задачках анализа выявляется логическая функция, реализуемая данной схемой. Синтез — это, напротив, построение схемы по данной конечной логической функции.