По данному табличному представлению автомата выстроить систему его команд.

Пусть конечный автомат имеет алфавиты X = {a, b}, Y = {а, b, с}, Q = {1, 2, 3}, а автоматные функции задаются таблицами:

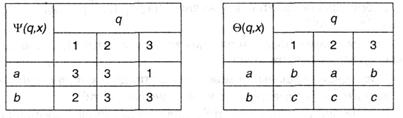
Выставленные две таблицы можно соединить в одну, условившись в каждую клеточку на первую позицию ставить значение Y(q_r, x_k), а через запятую на вторую позицию помещать значение Q(q_r, x_k). В итоге получится последующая «сводная» таблица:

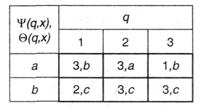
Видно, что таблица стала очень припоминать таблицу, задающую многофункциональную схему машины Тьюринга (см. п.7.3.3). Из нее просто просматриваются команды преобразования, осуществляемые данным автоматом:

Пусть на исходном такте автомат находится в состоянии q₀ = 1 и на его вход в следующие такты подается последовательность abb. Пользуясь списком команд можно установить, что автомат конвертирует эту последовательность в bсс и при всем этом окажется в состоянии 3.

Другой вариант описания автоматных функций — графический. Он обладает большей наглядностью, чем табличный. Состояния автомата <X, Y, Q, Y, Q> задается средством нацеленного графа, который именуется диаграммой (поточнее, диаграммой Мура). Верхушки графа помечены знаками из алфавита состояний автомата Q, а каждой команде q_ix_r → q_jy_s соответствует ребро, идущее из верхушки q_i в верхушку q_j, при всем этом ребру приписывается метка x_ry_s. Таким образом, ребро появляется в этом случае, если автомат, находящийся в состоянии q_i, средством некого входного сигнала x_r может быть переведен в состояние q_j. Если таковой перевод вероятен при нескольких входных воздействиях (х_г)⁽¹⁾….. (х_r)^(п), и при всем этом формируются выходные сигналы (y_s)⁽¹⁾,…, (y_s)^(п), то ребру приписывается выражение ((х_r)⁽¹⁾, (y_s)⁽¹⁾) v ((х_r)⁽²⁾, (y_s)⁽²⁾) v…v((x_r)⁽ⁿ⁾,(y_s)⁽ⁿ⁾.

Для диаграмм, представляющих конечный автомат, справедливы последующие утверждения:

1. из одной верхушки не может выходить 2-ух ребер с схожим входным эмблемой (условие однозначности);
2. если при работе автомата реализуется входная композиция q_ix_r, то непременно существует ребро, идущее из верхушки q_i помеченное эмблемой х_r (условие полноты);
3. количество вершин и ребер диаграммы является конечным.